CHAMP DE GRAVITE
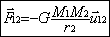
| [G] | = | [force] . [longueur]2 / [masse]2 | |
| = | kg.m.s-2 . m2 . kg-2 | ||
| = | m3 . kg-1 . s-2 |
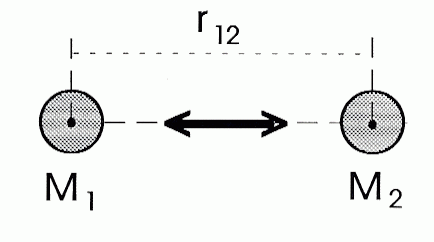
les forces gravitationnelles F1 et F2 valent : F1 = F2 = F = GMm / r2 où r est la distance entre la grosse et la petite masse.
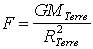
| Avec RTerre = 6400 km, on trouve : | MTerre = 6 1024 kg |
et surtout : | |
Compte tenu du fait que la densité des roches que l'on trouve à la surface de la Terre est de l'ordre de 3.3, cette mesure met en évidence la presence de matière cachée plus dense dans la Terre. C'est bien sur son noyau (constitué principalement de fer).
3/ Champ de gravité créé par une masse
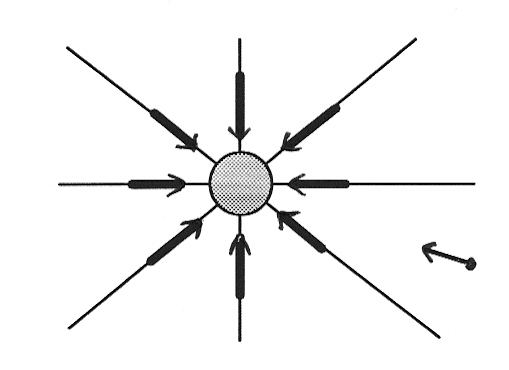
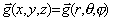 ( = GM/r2 dans ce cas particulier) toute particule de matière de masse m, placée dans ce champ g, subira une force de gravitation F = m g
( = GM/r2 dans ce cas particulier) toute particule de matière de masse m, placée dans ce champ g, subira une force de gravitation F = m g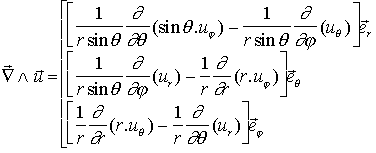

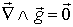
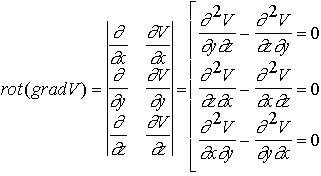
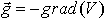 Le rotationnel de g sera alors automatiquement nul, par construction. On dit que g dérive d'un potentiel, et que V est le potentiel de gravité.
Le rotationnel de g sera alors automatiquement nul, par construction. On dit que g dérive d'un potentiel, et que V est le potentiel de gravité. 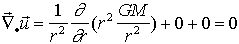
| On a donc : div g = 0 | <=> | div(grad(V)) = 0 |
| <=> | Laplacien(V) = 0 |
Le potentiel de gravité peut donc s'écrire sur la base des harmoniques sphériques :
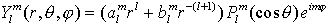
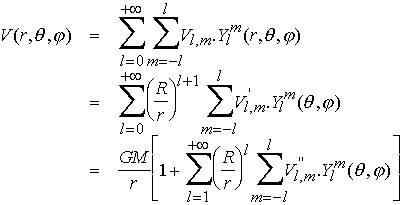
Au premier ordre (l=0), on retrouve bien le potentiel sphérique V = GM/r. Les termes suivants représentent donc des perturbations par rapport à ce potentiel simple qui serait celui d'une planète à symétrie sphérique.
La dépendance radiale du potentiel de gravité est donnée par le terme en (R/r)l+1 qui indique que plus on s'éloigne de la source du champ, plus les ondulations à courtes longueur d'onde sont lissées. On retrouve donc un potentiel sphérique si on s'éloigne suffisement de la planète (r >> R).
Le choix comme référentiel de description d'un repère dont l'origine est le centre de masse de la planète, permet d'annuler les termes de degré l=1, qui correspondent à un décalage du centre du potentiel (centre de masse) suivant chacun des trois axes.
b) potentiel hydrostatique
Les premiers calculs sur la forme du champ de gravité (et du potentiel) terrestre datent du début du XVIIme siècle. (Newton, 1642-1727; Huygens 1629-1695). L'idée est que la Terre en rotation doit être en équilibre hydrostatique. C'est à dire qu'elle se comporte à la longue comme un solide déformable soumis aux forces de gravité et à la force centrifuge : c'est à dire qu'elle s'aplatit aux poles. Il est facile de réaliser qu'une telle hypothèse conduit à proposer pour la Terre un potentiel de la forme :
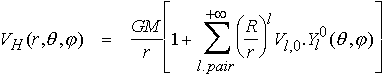
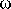
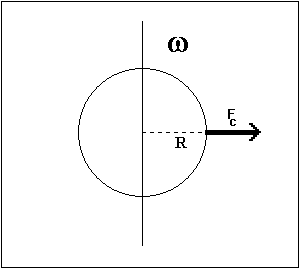 |
à l'équateur, la force centrifuge due à la rotation |
L'aplatissement théorique, c'est à dire la différence des rayons équatorial et polaire rapportée au rayon moyen, est de l'ordre de 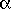 . Avec les valeurs précédentes et
. Avec les valeurs précédentes et 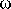 de l'ordre de 1 tour par 24 heures, on trouve
de l'ordre de 1 tour par 24 heures, on trouve 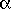 ~ 1/290 ce qui correspond à un aplatissement d'une vingtaine de km.
~ 1/290 ce qui correspond à un aplatissement d'une vingtaine de km.
c) Géoïde non-hydrostatique
La différence entre le potentiel observé (V) et le potentiel hydrostatique prédit à partir des équations (VH) est le potentiel non-hydrostatique (VN-H).
On peut dessiner les surfaces sphériques équipotentielles, c'est à dire les surface sur lesquelles le potentiel de gravité est constant.
A la surface de la Terre les océans (eau liquide) suivent une telle surface équipotentielle de gravité (une foi filtrés les effets des marées, des vagues, des courants, des différences de température et de salinité, etc...). Cette surface, la surface équipotentielle qui se confond avec le niveau moyen des mer, est nommée Géoïde.
Ce géoïde peut être donné en unité de potentiel ([GM/R] = m2 s-2) ou tout simplent en altitude. Il suffit de diviser le potentiel par le champ moyen <g> ([<g>] = m s-2) pour obtenir une unité en mètres. la valeur du géoïde (V( ,
,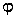 )/<g>) est donc tout simplent l'altitude de la surface équipotentielle.
Bien entendu, on peut comme pour le potentiel, définir un géoïde hydrostatique et un géoïde non-hydrostatique. Les ondulations de ce géoïde non-hydrostatique sont révélatrices d'anomalies de densité à la surface de la Terre et en profondeur.
)/<g>) est donc tout simplent l'altitude de la surface équipotentielle.
Bien entendu, on peut comme pour le potentiel, définir un géoïde hydrostatique et un géoïde non-hydrostatique. Les ondulations de ce géoïde non-hydrostatique sont révélatrices d'anomalies de densité à la surface de la Terre et en profondeur.
|
 = 1/298.259) = 1/298.259)
|
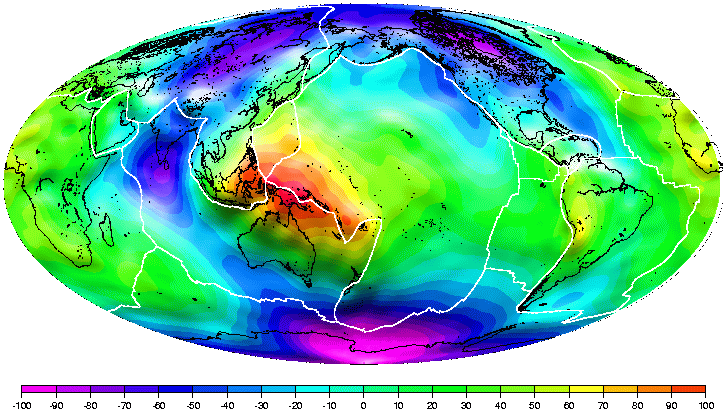
La figure ci-dessus montre une carte du Géoide. Les zones rouges montrent les zones où la gravité est plus forte et donc le Géoide plus haut. A l'inverse, les zones bleues sont celles où la gravité est moins forte, et le géoide plus bas. Le Géoide a cette forme caractéristique que l'on nomme "en forme de balle de Tennis". Une bande équatoriale positive est coupée par une bande longitudinale négative à la longitude de l'Inde.
6/ Définition de l'altitude et Déviation de la verticale
|
GRAND JEU CONCOURS avec un grand merci à Hergé | ||
|

| |
| vous avez compris | vous n'avez pas compris | |
| Tableau des amplitudes de chaque degré et de sa valeur relative dans la reconstitution. | ||||||||||
| degré | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| al | 33.7 | 18.9 | 9.95 | 7.45 | 5.79 | 4.74 | 3.11 | 2.73 | 2.28 | 1.62 |
| a2l / A2 | 65.32% | 20.62% | 5.69% | 3.19% | 1.93% | 1.29% | 0.56% | 0.43% | 0.30% | 0.15% |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 0.94 | 1.45 | 0.89 | 0.98 | 0.85 | 0.76 | 0.74 | 0.53 | 0.50 | 0.61 | 0.48 |
| 0.05% | 0.12% | 0.05% | 0.05% | 0.04% | 0.03% | 0.03% | 0.02% | 0.01% | 0.02% | 0.01% |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
| 0.42 | 0.41 | 0.30 | 0.31 | 0.23 | 0.26 | 0.23 | 0.22 | 0.21 | 0.20 | 0.24 |
| 0.01% | 0.01% | 0.01% | 0.01% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
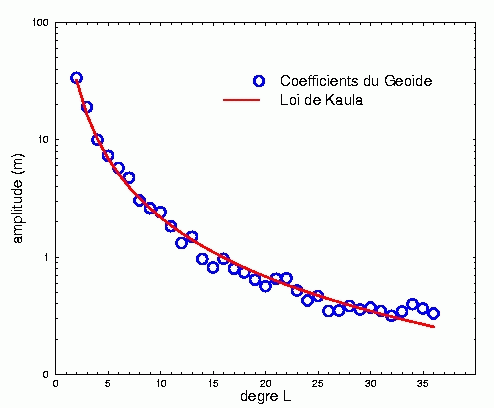 |
| Spectre du Géoide. L'amplitude (en m) de chaque degré est calculées d'après la formule donné au chapitre harmoniques sphériques. L'échelle des amplitudes est logarithmique. |
Le spectre du géoïde suit une loi empirique dite loi de Kaula : l'amplitude des coefficients varie en 1/l2. Les degrés élevés (petites longueur d'ondes) ayant une amplitude beacoup plus faible que les petits degrés (grandes longueurs d'ondes), la surface du Géoide est assez lisse: Les petits détails sont peu visibles par rapport aux grandes ondulations. Cette décroissance quadratique rend légitime la décomposition en harmoniques sphériques jusqu'à un degré l fini et pas trop élevé (36 par exemple).
b) spectre du champ de gravité et du géoïde a différentes altitudes
Si on reprend l'expression du potentiel sur la base des harmoniques sphériques exprimé plus haut :
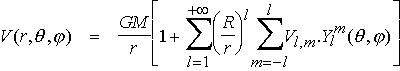
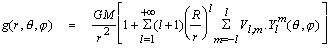
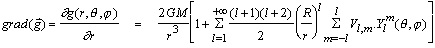
L'expression de g indique que le spectre du champ à la surface de la Terre est amplifié par un facteur (l-1) par rapport au spectre du potentiel à l'altitude 0. De même, l'expression du gradient du champ, montre que celui ci est amplifié par un facteur (l-1)(l+2) et atténué par un facteur (R/r)l.
 |
|
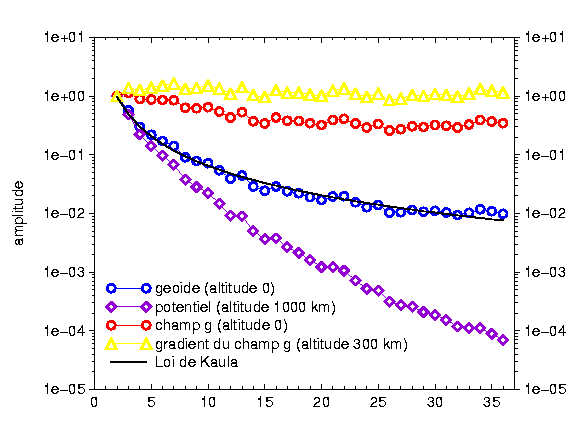
Spectre des différents champs à différentes altitudes. L'échelle des amplitudes est logarithmique et artificiellement ramenée à la meme origine pour toutes les courbes.
|
Il ressort du graphique ci dessus, que si le spectre du géoide suit la loi de Kaula (décroissance des termes de degré l en fonction de 1/l2), le potentiel à haute altitude (1000 km) décroit encore plus vite, alors que le champ ne décroit qu'en 1/l, et que le gradient du champ à une amltitude de 300 km a un spectre quasiment plat. En conséquence, si l'on veut connaitre les courtes longueurs d'onde du potentiel, il faut mesurer le gradient du champ, alors que si l'on veut connaitre les grandes longueurs d'onde il vaut mieux mesurer le potentiel directement et à haute altitude. Les grandes longueurs d'ondes (les premiers termes du développement en harmoniques sphériques) sont données par l'observation des orbites des satellites artificiels autour de la Terre. Par exemple STARLETTE (CNES 1975) ou LAGEOS (NASA 1976). Un satellite va "rouler sur la tole ondulée" qu'est l'équipotentielle du champ de gravité à l'altitude à laquelle il se trouve. Pour autant, ce mouvement n'est pas simple.
Le problème du satellite articifiel fait partie des problèmes en : d2x/dt2 + w.dx/dt = F(x,dx/dt, + parametres). En gros il suivra une trajectoire en fonction d'un champ de gravite qui, pour lui (le petit satellite), est module par la rotation diurne de la Terre. Les perturbations à petites périodes (conséquences des hétérogénéités de densité à petite longueur d'onde de la Terre) seront donc le long de la trajectoire en T, 2T, 3T, 4T, etc (T etant la periode de revolution orbitale), termes modulés aussi par la rotation Q de la Terre (Q étant plus grande en general que T: exemple T=6700sec pour un satellite a 1350 km et Q=86164sec). Cela donnera donc des perturbations avec des periodes en : (n.T±m.Q). A la fin, il "suffit donc" de mesurer la position d'un satellite qui orbite autour de la Terre (avec un laser par exemple) pour déterminer l'équipotentielle à l'altitude du satellite et partant, le Géoide.
c) mesure du géoïde
Les longueurs d'ondes plus courtes sont données par les mesures des satellites altimétriques au dessus des océans. Par exemple SEASAT (NASA) ou TOPEX-POSEIDON (CNES/NASA) ou tout récement JASON. La mer étant liquide, comme on l'a dit plus haut elle suit le Géoide (c'est meme la définition du Géoide : la surface moyenne des océans). Si l'on mesure depuis un satellite la hauteur de l'eau par rapport à l'orbite du satellite (avec un radar par exemple), alors on mesure directement la hauteur du Géoide !
Plus récemment, des satellites portant des accéléromètres ont été lancés (ex. CHAMPS). Ils sont dédiés à la mesure directe du gradient du champ de gravité à l'altitude du satellite. Enfin, le lien qui sépare deux satellites orbitants sur la même trajectoire l'un derrière l'autre (mesure de la distance ou de la vitesse relative entre les deux satellites; ex. GRACE) est corrélé avec les structures fines du champ, voire de la topographie si, bien entendu, ils sont suffisamment bas.
d) corrélation entre le géoïde et la topographie terrestre
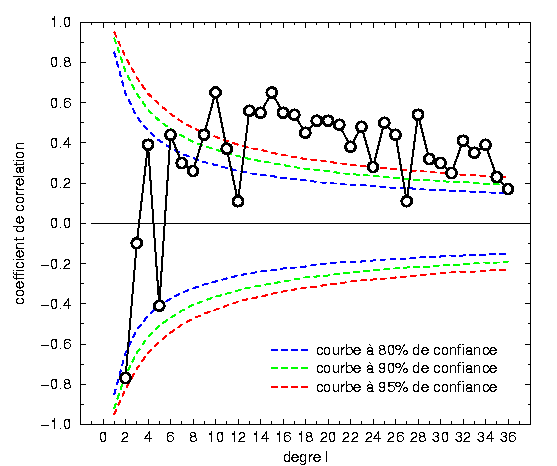 |
| Corrélation entre Géoide et Topographie terrestre. |
La corrélation est significative à petite longueur d'onde (l grand), et non significative à grande longueur d'onde (l petit). On en déduit que le géoïde à au moins deux sources différentes :
e) corrélation entre le géoïde et la tomographie sismique
Il est parfaitement clair qu'au niveau de l'Inde il y a un très bonne anti-corrélation entre Géoide et tomographie sismique. Ce sont bien les anomalies de masses détectées dans le manteau profond qui crée les ondulations du Géoide. En apparence, il y a une contradiction majeure : là où se trouvent des anomalies de masse plus dense, le géoide est moins élevé, ce qui correspond à une gravité plus faible !
En fait, cette contradiction n'est qu'apparente : il ne faut pas oublier que le manteau terrestre est visqueux, c'est à dire qu'il se déforme. Une masse dense va avoir tendance à s'enfoncer dans le manteau. Ce faisant, la surface va s'incurver vers le bas, comme aspirée par le courant descendant. Du coup , un déficit de masse apparait en surface. Ce déficit est plus faible que la masse en profondeur, mais comme il est plus près de la surface, son effet sur le Géoide (l'équipotentielle de gravité à la surface) est plus important !
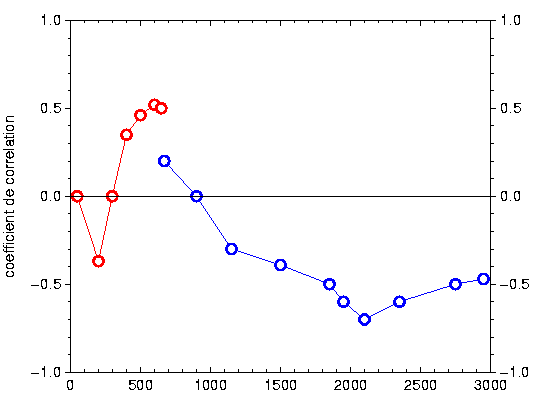
La courbe ci dessus montre le coefficient de corrélation total (sommé sur tous les degrés l) entre le géoïde observé et le géoïde synthétique calculé à partir des anomalies de densité dans le mateau à une profondeur donnée. C'est la vérification quatitative de l'Anticorrélation au niveau de l'Inde. Il apparait clairement que ce sont les anomalies de densité situées dans le manteau inférieur qui sont à l'origine des ondulations du Géoide. Il existe aussi une petite zone où il y a corrélation : la base du manteau inférieur. A cet endroit, l'effet décrit plus d'aspiration de la surface vers le bas ne joue plus : la masse est "posé sur le plancher" au lieu d'etre "suspendue au plafond".
GRAVIMETRIE
Les "anomalies" de masse sur et dans la croute sont la source premières des anomalies du champ de gravité en surface (à courte longueur d'onde). Dans la suite on va se placer systématiquement dans une approximation plane: l'extension géographique est suffisemment faible pour négliger la courbure de la Terre. Un grand nombre de problèmes se rapportent en fait à l'anomalie de gravité créée par une masse enterrée à une certaine profondeur. Nous allons donc étudier cette situation dans le cadre le plus simple possible.
On voit une corrélation significative à deux profondeurs :
SOMMAIRE
1/ Anomalie due à une sphère enterrée
|
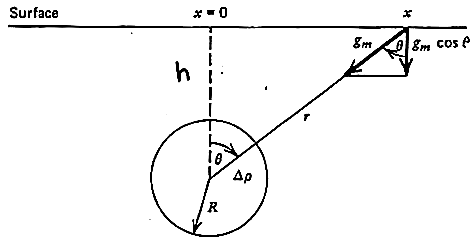
la sphère de rayon R et de densité
|
 |
|
|
Le champ gM créé par la sphère à une distance r (r>>R) vaut donc: 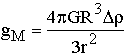
|
En première approximation, le champ terrestre g est perpendiculaire à la surface considérée plane. On considère donc l'anomalie verticale créée par la sphère.
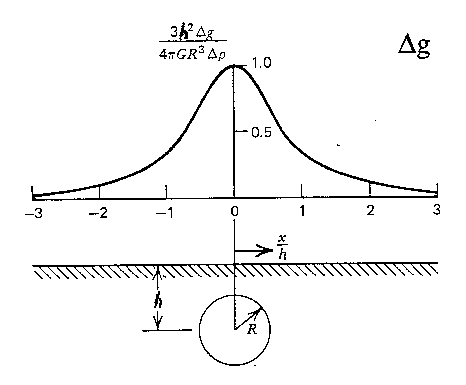 | 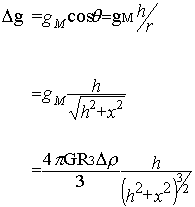 |
le sel ayant une densité d'environ 2200 kg/m3 et les sédiments aux alentours environ 2400 kg/m3, on obtient un 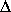
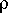 de 200 kg/m3.
de 200 kg/m3.
On trouve alors que R vaut environ 4 km.
On voit donc que le fait de mesurer l'anomalie gravimétrique au dessus d'une masse anormale enfouie permet de déterminer sa profondeur et son extension si on suppose connue sa densité. On conçoit l'interet de ce genre de méthodes pour la prospection minière, pour laquelle la profondeur de forage et la taille du gisement sont des paramètres critiques de la viabilité économique de la mise en exploitation.
a) correction latitudinale
La Terre étant un ellipsoide aplatit aux poles, si l'on fait une mesure de g à différentes latitudes on va trouver différentes valeurs sans que cela ne soit du à des variations locales dans la croute, mais simplement du au fait que l'on séloigne (ou que l'on se rapproche) du centre de la Terre. L'applatissement étant de l'ordre de 20 km par rapport au rayon moyen de 6400 km (donc 0.3 %), l'effet sur la gravité est du meme ordre, c'est à a dire environ 3 cm/s2 (3.10-3g).
De plus, la Terre étant en rotation (c'est meme l'origine de son applatissement), un corps placé à la surface subit une force centrifuge qui tend à l'expulser vers l'extérieur, et qui joue donc contre la gravité. Cette force dépend de la distance à l'axe de rotation, c'est à dire là aussi de la latitude (nulle aux poles, et maximum à l'équateur).
Si on veut pouvoir comparer des mesures à des latitudes différentes il faut corriger de ces deux effets. c'est la correction latitudinale. Il est facile d'écrire analytiquement ce que devrait valoir le champ de gravité g0 à la surface d'un ellipsoide applatit aux poles et en rotation :
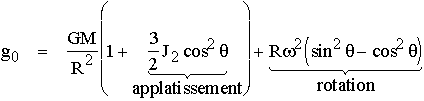
g0 est le champ de référence en tout point à la surface de la Terre. En développant cette formule avec des valeurs numériques données pour le rayon moyen de la Terre (R), son applatissement (J2), et sa vitesse de rotation (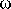 ), on trouve une valeur numérique pour le champ de référence en un point quelconque de la surface de la Terre. Dans le système GRS67, g0 vaut :
), on trouve une valeur numérique pour le champ de référence en un point quelconque de la surface de la Terre. Dans le système GRS67, g0 vaut :
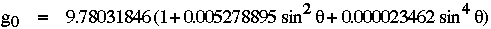
la dépendence en sin4 vient d'un modèle d'applatissement plus élaboré en J4.
vient d'un modèle d'applatissement plus élaboré en J4.
L'anomalie réduite sera donc la valeur mesurée moins cette valeur g0 de référence.
b) réduction à l'air libre - anomalie à l'air libre
Si on mesure le champ de gavité à différentes altitudes, il est la aussi "normal" de mesurer des valeurs de g différentes sans que cela n'ait rien à voire avec la croute (on s'éloigne simplement du centre de la terre). Pour pouvoir comparer des mesures effectuées à des altitudes différentes il faut corriger de cet effet.
si l'on se trouve sur le géoïde (altitude 0), g vaut : 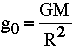 où R est le "rayon" de l'ellipsoide applatit.
où R est le "rayon" de l'ellipsoide applatit.
|
| 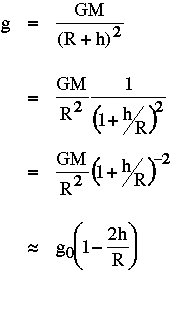
|
|
| 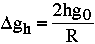
|
Une mesure de gravité corrigée de l'effet latitudinal et de l'altitude est nommée anomalie à l'air libre.
c) réduction topographique - anomalie de Bouguer
Il est clair que l'anomalie à l'air libre est entièrement dominée par la topographie: quand on se trouve à une certaine altitude h c'est en général parcequ'on a une montagne sous les pieds ! Il faut donc également tenir compte de l'effet du à la masse de cette montagne et pas seulement son élévation si l'on veut pouvoir detecter des anomalies gravimétriques générées par des anomalies de densités qui sont située plus profondement dans la croute.
En première approximation, on peut assimiler la masse de la topographie à celle d'un disque homogène de rayon R et de hauteur h. Que vaut g au dessus d'un tel disque ?
Le champ total sera donc la somme des champs créés par tous les anneaux possibles qui composent le cylindre (de rayon r variant entre 0 et R, et à une hauteur y variant entre 0 et h). C'est donc bien évidemment l'intégrale de dgy suivant h et r :
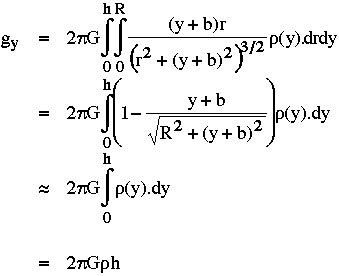
l'anomalie de gravité due au fait que l'on a une montagne sous les pieds vaut donc approximativement : 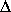 g = 2
g = 2
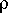 Gh
Gh
c'est l'anomalie de Bouguer (du nom du célèbre géodesien Français). Une carte de gravité corrigée de l'effet latitudinal, de l'effet d'élévation et de l'effet de topographie est dite carte d'anomalie de Bouguer.
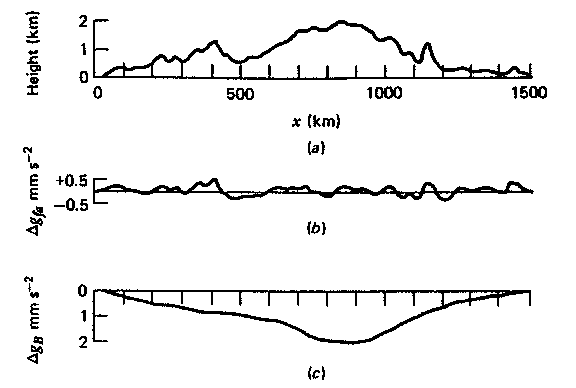
La figure suivante (gauche) montre des courbes de topographie (a), d'anomalie de gravité à l'air libre (b), et d'anomalie de Bouguer (c), sur le meme terrain. Il est clair que l'anomalie à l'air libre est corrélée et domminée avec et par la topographie à courte longueur d'onde. L'anomalie de Bouguer, elle est anti-corrélée avec la topographie à grande longueur d'onde. C'est la mise en évidence du phénomène de compensation : il y a en profondeur une anomalie de densité opposée à celle en surface. cette anomalie profonde joue le role d'un "flotteur" qui va maintenir à la surface l'exces de masse généré par la topographie.
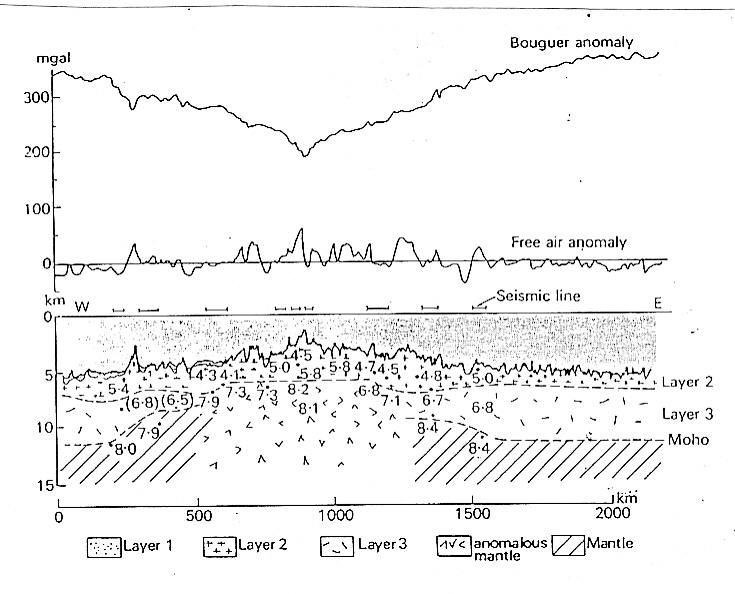
La figure de droite montre clairement la présence de manteau anormalement chaud (peu dense) en profondeur, visible à la fois dans l'anomalie de Bouger et dans le profil sismique.
|
|
| les différentes anomalies sur un terrain donné | anomalie à l'air libre et anomalie de Bouguer générées sur un terrain dont les anomalies de densité sont données par un profil sismique |
Une topographie impose un exces de masse à la surface. Une petite structure sera soutenue par la lithosphere et donnera un signal visible dans la carte d'anomalie à l'air libre mais pas d'anomalie de Bouguer.
Par contre, la lithosphere ne pourra pas soutenir élastiquement une grosse structure. La présence d'une racine plus légère sous la structure est indispensable pour maintenir celle ci à la surface. le bilan des masses à grande longueur d'onde est nul donc il n'y aura pas d'anomalie à l'air libre associée à des structures à grande longueur d'onde. Par contre, Il y aura une anomalie de Bouguer négative sur ces structures.
Il existe différents modèles de compensation :
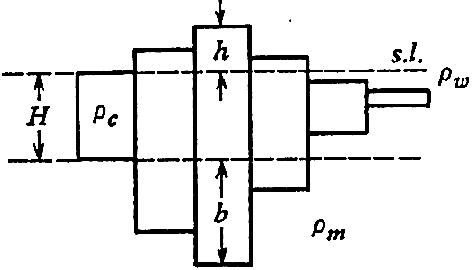 le modèle d'Airy |
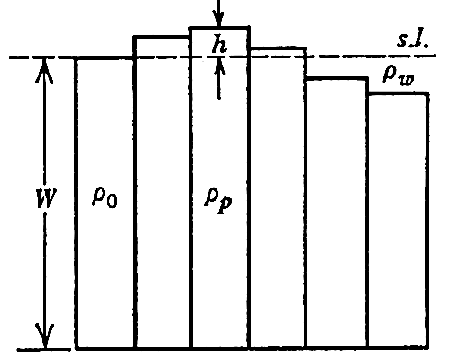 le modèle de Pratt |
Le modèle d'Airy considère que c'est de la croute normale de densité toujours identique (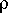 c) qui est épaissie sous une topographie quelconque de manière à créer un "flotteur" plus leger que le manteau qui l'entoure, qui va empecher la topographie de s'enfoncer.
c) qui est épaissie sous une topographie quelconque de manière à créer un "flotteur" plus leger que le manteau qui l'entoure, qui va empecher la topographie de s'enfoncer.
Le modèle de Pratt suppose au contraire que la profondeur atteinte par la couche mise en jeu est toujours identique (W), et que c'est la densité qui va changer pour permettre à une colonne plus légère de "monter" de manière à créer une topographie.
Dans ce contexte, le Modèle de Pratt correspond donc plutot à une analyse thermique (densité modifiée par effet thermique), et le modèle d'Airy à une analyse mécanique (croute normale déformée). Le champ de gravité ou le géoïde prédit par ces deux modèles seront évidemment différents.
De manière générale, on a : 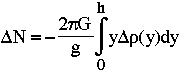
cette formule est analogue à la formule de l'anomalie gravimétrique créée par un cylindre (voire anomalie de Bouguer), dans laquelle on remplace g par son champ potentiel N. Comme l'élément différentiel de champ dg est proportionnel à 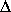
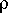 (y), dN est proportionnel à y
(y), dN est proportionnel à y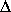
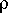 (y). On constate qu'on retrouve bien le champ si l'on calcule le gradient du potentiel. Ensuite il faut bien sur intégrer l'élément différentiel de potentiel sur tout le volume pour établir la formule ci-dessus.
(y). On constate qu'on retrouve bien le champ si l'on calcule le gradient du potentiel. Ensuite il faut bien sur intégrer l'élément différentiel de potentiel sur tout le volume pour établir la formule ci-dessus.
c'est l'intégrale de la densité suivant la profondeur qui va changer suivant le modèle considéré.