CHAMP DE VITESSES - TECTONIQUE DES PLAQUES
| Attention: ceci est un cours de niveau MASTER 1ere ou 2eme année, relativement exigeant du point de vue des mathématiques. Si vous vous interressez à la tectonique des plaques ou à la dynamique interne de la Terre sur un mode "vulgarisé" allez plutot LÀ! |
1/ Décomposition en harmoniques sphériques d'un champ vectoriel sur la sphère a) Ecriture d'un vecteur sur une sphère b) Décomposition en harmoniques sphériques c) Déivergence et rotationnel du champ de vitesse horizontal d) Exemples 2/ Tectonique des plaques a) Champ de vitesses en surface b) Spectres : Poloidal-Toroidal et Divergence-Rotationnel c) Sources de la tectonique des plaquesTout champ vectoriel dont la divergence est nulle, peut s'écrire sous la forme :
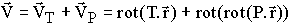
En fait cela vient d'une relation plus générale : tout vecteur de l'espace réel peut s'ecrire sous la forme :
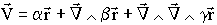
C'est à dire que l'on peut définir une base de trois vecteurs orthogonaux (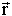
, 
, 
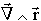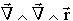) sur laquelle les 3 coefficients 
, 
, 
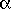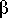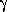sont les coordonnées du vecteur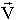 
On obtient l'expression des composantes à partir de l'expression du rotationnel en coordonées sphériques :
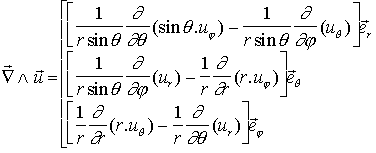
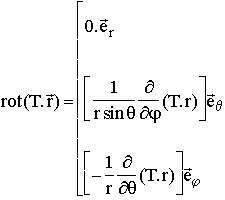
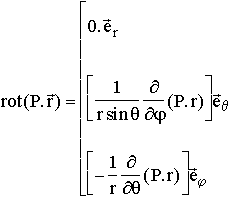
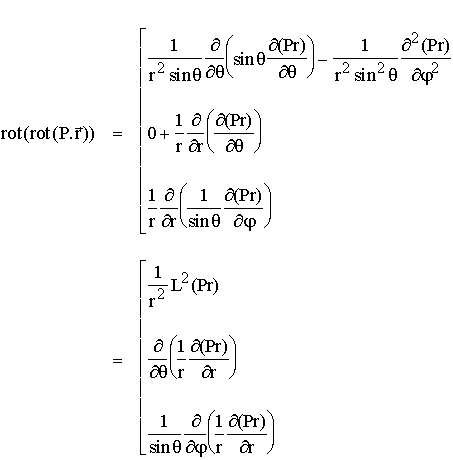
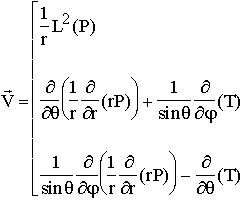
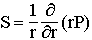, on obtient finalement :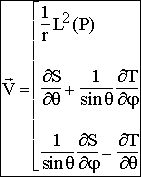
Quand on s'interesse à la tectonique des plaques, on a affaire à un champ essentiellement surfacique sur la sphère (composante radiale nulle), et on écrira les composantes du champ de vitesse (horizontal donc) sous la forme :
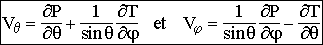
P et T sont des champs scalaires fonctions de 
et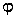 
.
P est le champ Poloïdal et T est le champ Toroïdal.
b) Décomposition en harmoniques sphériques
Les écritures précédentes font apparaitre les
dérivées des champs scalaires poloïdal (P) et
toroïdal (T) en fonction des angles et
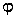. On peut donc, comme dans le
cas de la décomposition d'un champ scalaire, écrire la
décomposition d'un champ vectoriel sur la base, non plus des
harmoniques sphériques, mais des dérivées de
celles ci : la base des harmoniques sphériques généralisées.
On écrit donc :
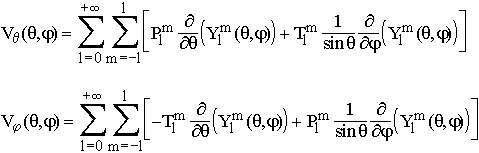
Les Plm
et Tlm sont les coefficients poloïdaux et
Toroïdaux de la décomposition de V en harmoniques
sphériques.
c) Divergence et rotationnel de champ de vitesse horizontal
La divergence horizontale du champ de vitesse ci dessus peut s'exprimer
comme suit :
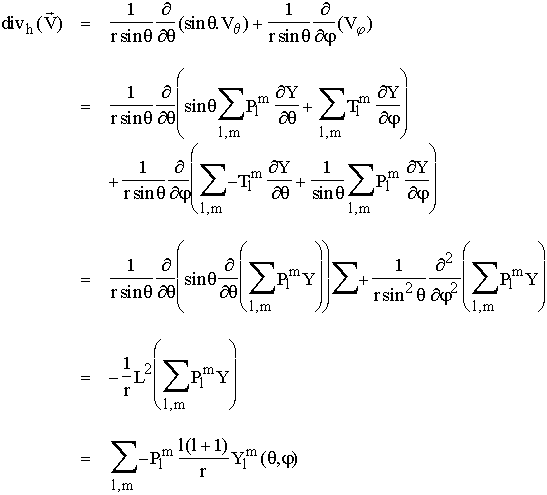
De la même façon, on obtient pour le rotationnel radial
(composante selon r), que l'on appellle également vorticité, du
champ de vitesse :
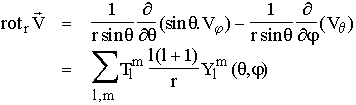
On voit donc que la divergence est liée uniquement au champ poloidal, alors que le rotationnel est lui uniquement lié au champ toroidal. Ces deux champs scalaires à partir desquels on peut reconstituer un champ vectoriel ont donc un sens physique très précis : l'un est la quantité de divergence présente dans le champ vectoriel, l'autre est la quantité de rotationnel.
d) Exemples
Champs de vitesses sur une sphère. Purement poloidal ou purement
toroidal de degré L=1.
Poloidal degré 1 | ||||||||||||||||||||||||||||||||||||||
 |  |
| ||||||||||||||||||||||||||||||||||||
Un champ purement poloidal est purement divergent. Si seul le degré
1 est activé, alors il s'agit d'un champ qui diverge à un pole et qui converge à l'autre, tout simplement !
Toroidal degré 1 | ||||||||||||||||||||||||||||||||||||||
 |  |
| ||||||||||||||||||||||||||||||||||||
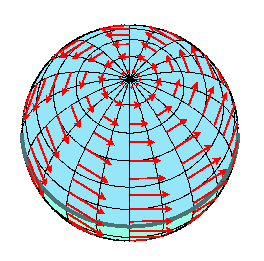Un champ purement toroidal est purement rotationnel. Si seul le degré
1 est activé, alors il s'agit d'un champ qui tourne sur toute la sphère, tout simplement !
2/ Tectonique des plaques
a) Champ de vitesses en surface
Poles de rotation des plaques, vitesses, divergence-rotationnel (vorticité)
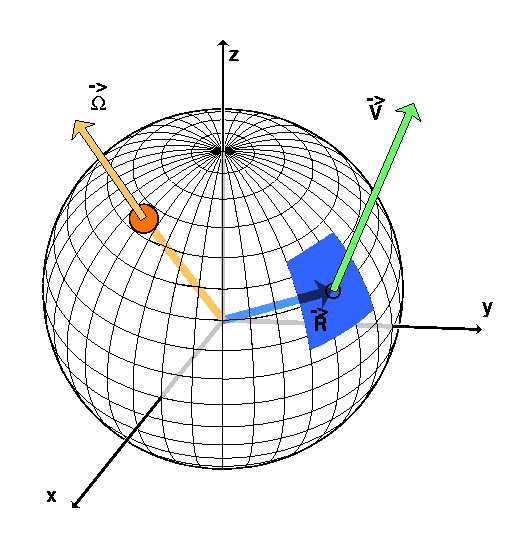
Tout déplacement sur la surface d'une sphère (ici la Terre) est assimilable à une rotation autour d'un axe vertical passant par un point situé quelque part sur la surface de cette meme sphère. la vitesse de n'importe quel point sur une plaque donnée dépend donc simplement de sa distance par rapport au pole de rotation de la plaque, et de la vitesse de rotation de celle-ci autour de celui là. La formule mathématique est la suivante :
| -> | -> | -> | ||
| V | = | R |  | |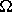
| ^ |
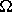est le vecteur rotation de la plaque
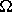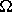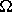Le vecteur peut etre défini par ces 3 composantes dans l'espace (X, Y, et 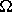Z). C'est un vecteur dont l'origine est le centre de la Terre et qui coupe la surface de la Terre en un point donné. Ce sont les coordonnées (latitude 
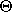et longitude 
) de ce point que l'on appelle le pole de rotation. La vitesse angulaire de rotation est tout simplement la longueur (la norme) du vecteur .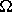
La table suivante donne les position des poles de rotation, ainsi que les vitesses de rotation autour de ces poles en degrés par million d'années, déterminés pour les 12 grandes plaques dans le modèle NNR-Nuvel-1a (DeMets et al, 1990, Argus et Gordon, 1991, et DeMets et al., 1994).
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
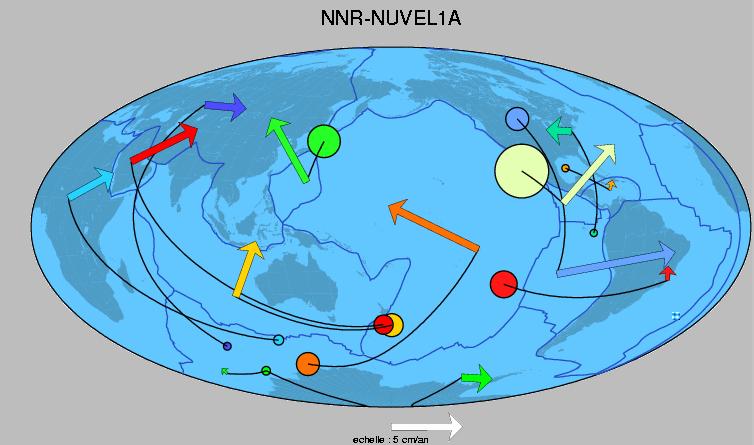
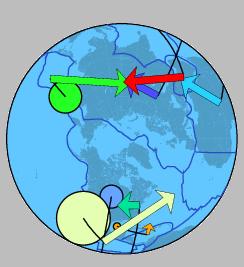
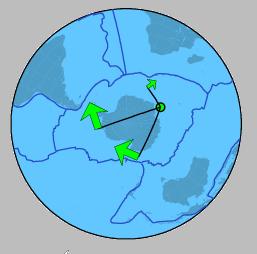
Grace aux formules détaillées plus haut, on peut donc décomposer le champ de vitesses à sa surface de la Terre (champ de vecteurs) en deux champs scalaires. Les descriptions sous la forme de vecteurs ou sous la forme de "somme" de deux scalaires est strictement identique puisque l'on peut passer de l'une à l'autre par une formule mathématique exacte.
 |  |
La première carte montre le champ Poloidal, qui est donc équivalent à la divergence
horizontale en surface du champ de vitesse. on voit clairement les zones où les
vitesses divergent (en rouge) : ce sont les dorsales, et les zones où les vitesses
convergent (en bleu) : ce sont les zones de subduction ou de collision.
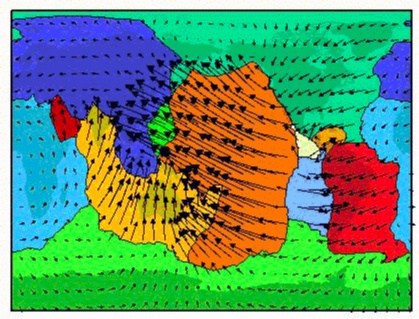
La deuxième carte montre le champ Toroidal qui est donc équivalent au rotationnel
autour d'un axe vertical. on voit les frontières entre les plaques quand elles
coulissent les unes le long des autres : cisaillement dextre (bleu) comme en Californie,
cisaillement senestre (rouge) comme en Papouasie-Nouvelle Guinée.
b) Spectres : Poloidal-Toroidal et Divergence-Rotationnel
Comme pour n'importe quel champ scalaire décomposé
sur la base des harmoniques sphériques, on peut calculer les spectres
des composantes du champ de vitesse.
|
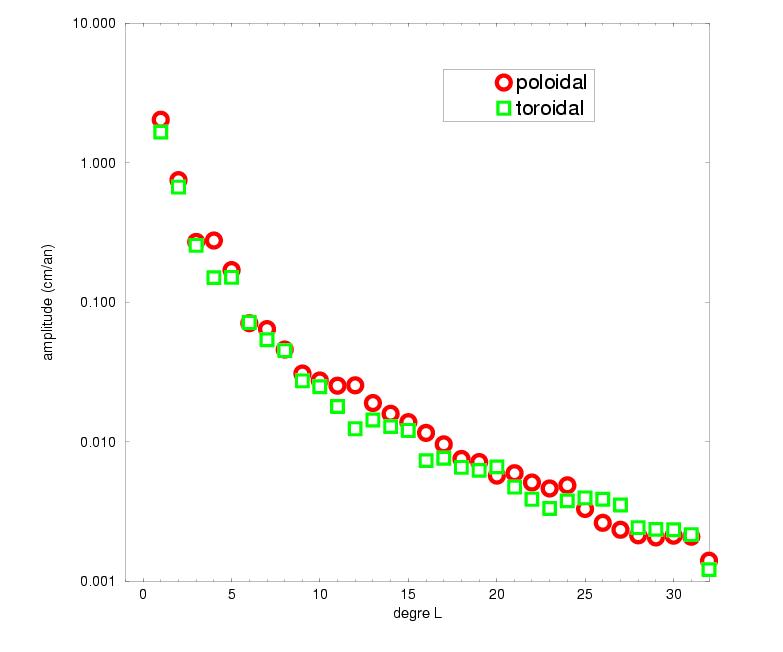
Il y a correspondance entre les spectres et la taille caractéristique des plaques. En effet, les "bosses" des spectres aux degrés 4 et 5 correpondent au maximum "d'énergie" dissipé par les plaques. Les plaques qui dissipent le plus d'énergie (qui ont le plus de longueur de dorsales) ont une taille caractéristique qui correspond au degré 4 ou 5 de la décomposition du champ de vitesse en harmoniques sphériques |
|
|||
|
plaque |
Surface x 106 km2 |
Taille caractéristique x 103 km |
Degré caractéristique |
|
|
Pacifique |
110 |
12 |
3 |
|
|
Amérique |
102 |
11 |
3 |
|
|
Afrique |
79 |
10 |
4 |
|
|
Eurasie |
70 |
9 |
4 |
|
|
Inde |
61 |
9 |
4 |
|
|
Antarctique |
60 |
9 |
4 |
|
|
Nazca |
17 |
5 |
7 |
|
|
Philippines |
6 |
3 |
13 |
|
|
Arabie |
5 |
3 |
13 |
|
|
Caraibes |
3 |
2 |
19 |
|
|
Coco |
3 |
2 |
19 |
|
|
|
||||
C'est la
nécessité de refroidir la Terre qui entraine des
mouvements de convection dans le manteau terrestre. La matière chaude monte,
apporte la chaleur à la surface. la Chaleur rayonne vers l'extérieur, la matière
en surface se refroidit, puis replonge dans le manteau où elle se réchauffe à nouveau et
recommence un nouveau cycle.
En l'absence de plaques rigides à la surface de la Terre, les mouvements dans le
manteau seraient purement poloidaux (c'est à dire divergent-convergent) sans toroidal
(c'est à dire sans cisaillement)
 |
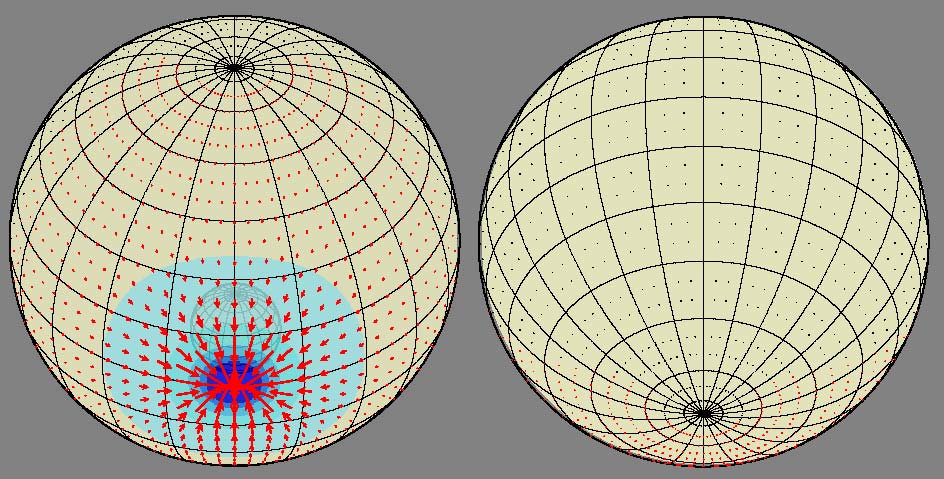Exemple de flux en surface crée par une anomalie de densité (thermique) qui s'enfonce dans le manteau terrestre. les niveaux de couleur montrent la divergence du champ de vitesse (vecteurs rouges). |
Les vitesses
en surface convergent toutes vers le "puits" créé par la masse qui s'enfonce. la
divergence de ce champ de vitesse en surface est localisée autour de ce point de
convergence. Il n'y a pas de rotationnel.
C'est la présence de plaques rigides à la surface qui entraine
la création de cisaillements, c'est à dire d'un flux toroïdal.
 |
Exemple de flux en surface crée par une anomalie de densité (thermique) qui s'enfonce dans le manteau surmonté de 2 plaques hémispheriques (1 verte, 1 bleue). les vecteurs rouges montrent le champ de vitesse. |
Du fait de la présence des plaques, le champ de vitesse est totalement différent : les plaques étant rigides
elles entrainent le manteau avec elles sous toute leur surface. La rigidification du champ a deux conséquences :
- les vecteurs devenant parallèles, du cisaillement apparait.
- des déplacements apparaissent sur toute la surface, et en particulier une zone divergente apparait
aux antipodes de la zone convergente.
 |
 |
| Divergence. | Rotationnel. |
| de l'écoulement en surface résultant du déplacement des deux plaques l'une vers l'autre. Dans le cas de la divergence (2 figures de gauche) les régions rouges sont en convergence (à la frontière des deux plaques, là où elles convergent l'une vers l'autre) les régions bleues sont en divergence (là où les plaques s'écartent l'une de l'autre). Dans le cas du rotationnel, on a du cisillement dextre (rouge) et senestre (bleu) près des poles , là où les plaques "tournent". | |
Un autre exemple avec une petite plaque découpée dans la litosphère, toujours entrainée par une anomalie de densité thermique enterrée. Le flux "rigidifié" montre que la déformation se concentre sur les frontières entre les plaques: les plaques elles meme étant rigides, divergence et rotationnel sont nuls sur la surface des plaques. Les frontières perpendiculaires au mouvement deviennent divergentes/convergentes, et les frontières parallèles deviennent cisaillantes (dextre et senestre). Le manteau visqueux se "passerait bien" du mouvement cisaillant qui freine la plaque alors qu'il ne transporte pas de chaleur. Il diminue donc l'efficacité de la machine thermique.
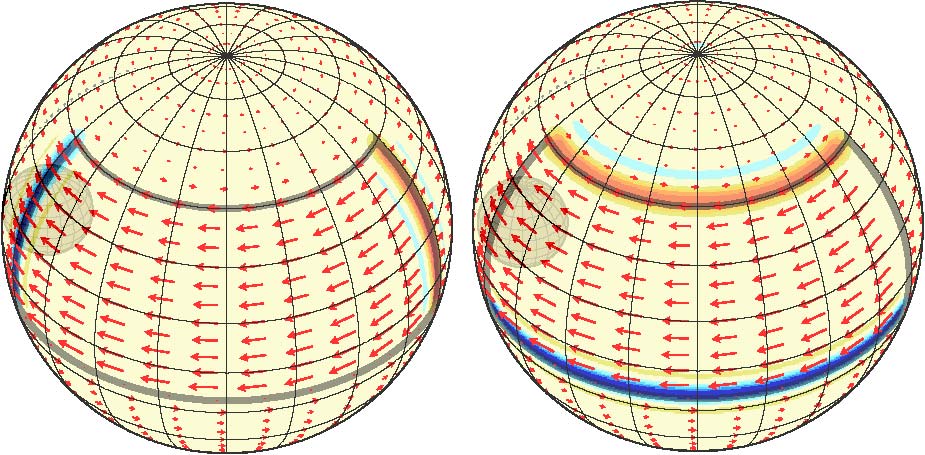
De plus, on peut calculer la répartition de l'énérgie cinématique entre les deux flux (toroïdal et poloïdal) en fonction de la profondeur.
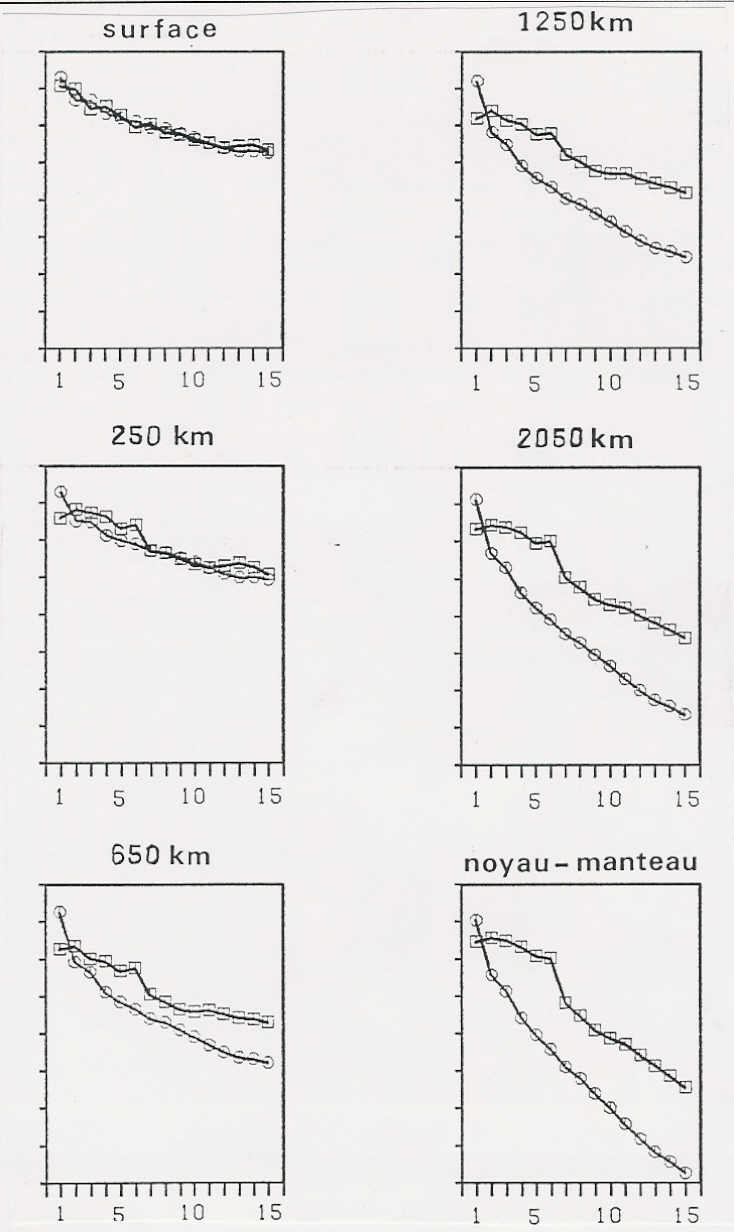
La figure montre clairement que l'amplitude du champ poloïdal est la même dans tout le manteau, alors que le champ toroïdal est maximum en surface et décroit avec la profondeur. Cela confirme que le champ toroïdal est créé en surface par la plaques alors que le champ poloïdal est créé partout par les anomalies thermiques
Retour au sommaire des cours