Champ de vitesse - tectonique des plaques

I/ décomposition en harmoniques sphériques d'un champ vectoriel sur la sphère

a) écriture d'un vecteur sur une sphère

Tout champ vectoriel dont la divergence est nulle, peut s'ecrire sous la forme :

En fait cela vient d'une relation plus générale : tout vecteur de l'espace réel peut s'ecrire sous la forme :

c'est à dire que a,b,g sont les coordonnées du vecteur sur la base (, , ).

On obtient l'expression des composantes à partir de l'expression du rotationnel en coordonnées sphériques :

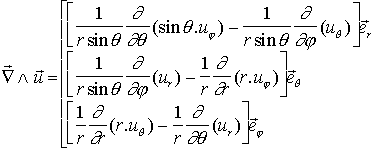
qui donne donc, d'une part:

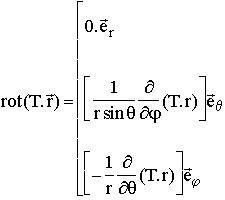
et d'autre part :

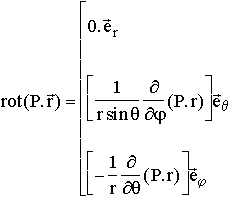
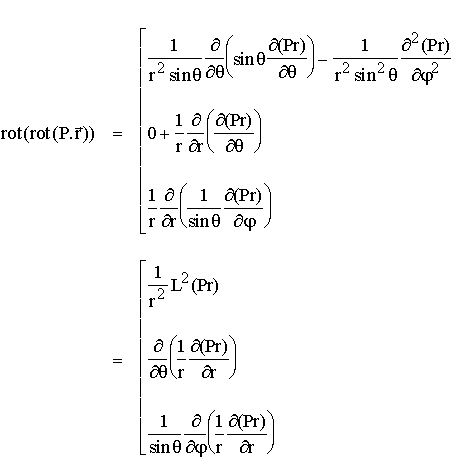
et donc :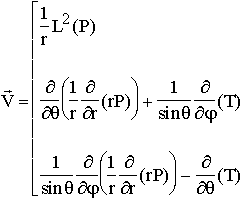

En posant , On obtient finalement :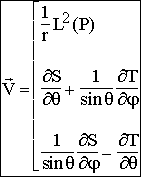

Quand on s'interesse à la tectonique des plaques, on a affaire à un champ essentiellement surfacique sur la sphère (composante radiale nulle), et on écrira les composantes du champ de vitesse (horizontal donc) sous la forme :

en faisant l'amalgame entre S et P.

P et T sont des champs scalaires fonctions de q et j. P est le champ Poloïdal et T est le champ Toroïdal.

b) décomposition en harmoniques sphériques

Les écritures précédentes font apparaitre les dérivées des champs scalaires poloïdal (P) et toroïdal (T) en fonction des angles q et j. On peut donc, comme dans le cas de la décomposition d'un champ scalaire, écrire la décomposition d'un champ vectoriel sur la base, non plus des harmoniques sphériques, mais des dérivées de celles ci : la base des harmoniques sphériques généralisées. On écrit donc :

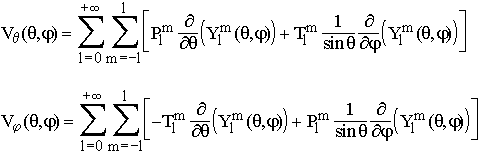
les P_l^m et T_l^m sont les coefficients poloïdaux et Toroïdaux de la décomposition de V en harmoniques sphériques.

c) divergence et rotationnel du champ de vitesse horizontal

La divergence horizontale du champ de vitesse ci dessus peut s'exprimer comme suit :

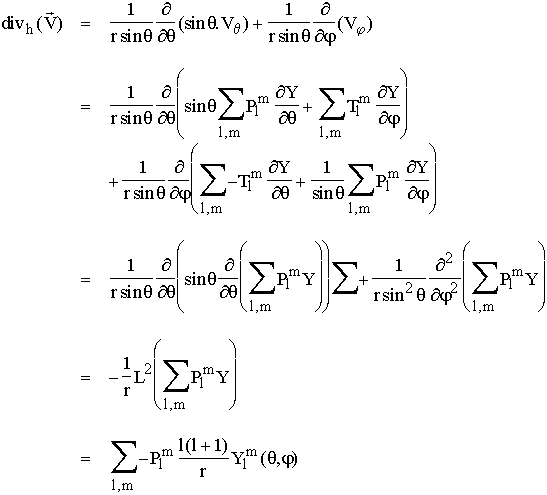
De la même façon, on obtient pour le rotationnel radial (composante selon r), que l'on appellle également vorticité, du champ de vitesse :

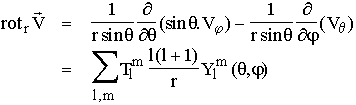
d) exemples

Champs de vitesses sur une sphère. Purement poloidal ou purement toroidal de degré L=1.

II/ Tectonique des plaques

a) champ de vitesse en surface : poles de rotation des plaques, vitesse, divergence, et rotationnel (vorticité)

b) Spectres : poloïdal-Toroïdal et divergence-rotationnel

Il y a correspondance entre les spectres et la taille caractéristique des plaques. En effet, les "bosses" des spectres aux degrés 4 et 5 correpondent au maximum "d'énergie" dissipé par les plaques. Les plaques qui dissipent le plus d'énergie (qui ont le plus de longueur de dorsales) ont une taille caractéristique qui correspond au degré 4 ou 5 de la décomposition du champ de vitesse en harmoniques sphériques.

c) sources de la tectonique des plaques

C'est la nécéssité de refroidir la Terre qui entraine des mouvements de convection dans le manteau terrestre. En l'absence de plaques les mouvements dans le manteau seraient purement poloidaux.

Exemple de flux crée par une anomalie de densité (thermique) qui s'enfonce dans le manteau terrestre.

C'est la présence de plaques rigides à la surface qui entraine la création de cisaillements, c'est à dire d'un flux toroïdal.

Exemple de flux crée par la même anomalie de densité qui s'enfonce dans le manteau terrestre surmonté de deux plaques hémisphèriques.

De plus, on peut calculer la répartition de l'énérgie cinématique entre les deux flux (toroïdal et poloïdal) en fonction de la profondeur.

La figure montre clairement que l'amplitude du champ poloïdal est la même dans tout le manteau, alors que le champ toroïdal est maximum en surface et décroit avec la profondeur. Cela confirme que le champ toroïdal est créé en surface par la plaques alors que le champ poloïdal est créé partout par les anomalies thermiques