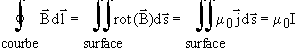Champ Electrique - Champ magnétique

I/Charge électtrique - Loi de Coulomb

1/ répulsion réciproque de deux charges

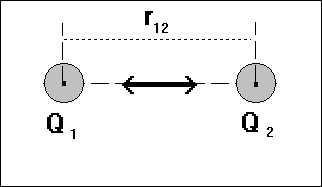
Les deux charges Q₁ et Q₂ se repoussent mutuellement avec une force F₁₂ telle que :

où 1/4pe₀ est la constante de proportionnalité: 1/4pe₀ = 8.9875 10⁹ (S.I.)

e₀ = 10^-9 / 36p (S.I.)

e₀ = 8.85 10^-12 (S.I.)

[1/4pe₀] = [force] . [longueur]² / [charge] ²

= kg.m.s^-2 . m² . Coulomb^-2

= kg.m³.s^-2. .A^-2 s^-2 (1 Coulomb est la charge transportée par un courant de 1 ampère en 1 seconde)

= kg.m³.s^-4.A^-2

2/ determination de e₀ : expérience de Coulomb

Comme dans l'experience de Cavendish pour la gravité, chacune des charge exerce une répulsion sur l'autre, ce qui provoque une rotation du pendule. Il suffit de mesurer la rotation de la "balance de Coulomb" pour en déduire la force d'interaction des deux charges...

3/ champ Electrostatique créé par une charge

Dans le champ de ainsi créé : dans ce cas particulier) toute particule de charge q placée dans ce champ E, subira une force de électrostatique (ou électromotrice) : F= q E

Dans la conception de la notion de champ, une particule, ou un groupe de particules) crée dans tout l'espace "quelque chose", de sorte que l'espace n'a plus pour seule propriété d'être vide : En effet, si on place une autre particule chargée en un point, elle "réagira" à cette nouvelle propriété de l'espace par le fait qu'elle se trouvera soumise à une force.

4/ champ magnétique - force de Lorentz - force de Laplace

Les effets magnétiques sont connus depuis l'antiquité. Par contre la relation entre phénomènes magnétiques et électricité est beaucoup plus récente (expérience fondamentale d'Oersted en 1820 qui montre qu'une aiguille aimantée placée au voisinage d'un fil parcouru par un courant électrique s'oriente selon une direction perpendiculaire au fil).

Avant cette période, il y avait confusion entre phénomènes magnétiques et phénomènes électrostatiques. En fait ces phénomènes sont indépendants en ce sens qu'un aimant n'a pas d'influence sur les interactions de corps chargés immobiles et que les corps chargés immobiles n'exercent pas d'influence sur les aimants.

Mais, les courants électriques étant dus à des mouvements de charges, le phénomène fondamental est celui de l'action exercée sur une particule chargée en mouvement.

dans un espace ou règne du "magnétisme"

1-	tout l'espace est influencé	=>	présence d'un champ magnétique B
2-	il existe des trajectoires de particules chargées qui ne sont pas influencées par ce champ	=>	ce champ est vectoriel : B
3-	pas d'accélération le long de la trajectoire	=>	force créée par ce champ perpendiculaire à la trajectoire : v B
4-	accélération perpendiculaire proportionnellle à la charge	=>	force proportionnelle à la charge q

on en déduit la formule de Lorentz :

Bien sur, si E règne aussi :

par habitude (toujours très mauvais) et par analogie (toujours dangereux), on parle de champ électromoteur (E_m) pour le produit vectoriel v B. Ainsi la force de Lorentz résulterait de la somme de deux champs : le champ électrostatique et le "champ" électromoteur.

Mais attention : E_m n'est pas un vrai champ puisqu'il dépend de la vitesse de la particule sur laquelle il s'applique !

Remarque : La force de Lorentz ne travaille pas (elle est toujours perpendiculaire au déplacement). Il n'y a donc pas de dissipation d'énergie associée à cette force. c'est une caractéristique importante qui aura son importance dans les problèmes de champ magnétique terrestre et de dynamo.

unité de B :

[B] = [force] / [charge] / [vitesse]

= kg. m. s^-2 (Coulomb) ^-1 m^-1 .s

= kg s^-2 A^-1

= Tesla ou Gauss

1 Tesla (physicien yougoslave 1857-1943), c'est donc le champ qu'il faut pour qu'une particule de 1 coulomb se déplaçant à 1 m/s subisse une force de 1 Newton (équivalente à un poids de 100 grammes à la surface de la Terre) c'est donc un champ assez intense ! (un gros électro-aimant produit en général un champ de quelques Tesla)

1 Gauss (mathématicien allemand 1777-1855), vaut 10^-4 Tesla (c'est à dire que ca correspond à un poids de 1 centième de gramme)

Dans la suite, on verra que le champ Terrestre actuel prend des valeurs de l'ordre de quelques fraction de Gauss (0.2 à 0.4), alors que l'aimantation rémanentes des roches représente quelques fractions de 10^-5 Gauss (ou quelques nano Tesla)

La formule de Lorentz permet de calculer la force subie par un élément de volume d'un conducteur (dt) entourant un point M, et parcouru par un courant de densité j.

r_m étant la densité volumique de charge des porteurs mobiles et v leur vitesse au point M. L'élément dt contient la charge dq, qui subit la force magnétique dF :

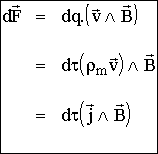
Si on considère un élément de conducteur filiforme, de section constante, assez petit pour que le champ magnétique soit constant sur toute sa longueur, alors :

le volume du cylindre est : dt = dS.dl

il est donc soumis à la force :

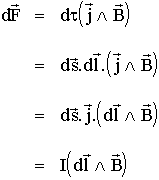
F est donc la force à laquelle est soumis tout conducteur placé dans un champ B. c'est la force de Laplace. Elle est :

- proportionnelle à l'intensité du courant

- proportionnelle à l'intensité du champ magnétique B

- perpendiculaire au fil

- perpendiculaire au champ magnétique

le sens de F est donné par le produit vectoriel, ou encore la règle du bonhomme d'Ampère.

5/ champ magnétique créé par un courant : Loi de Biot et Savart

Revenons à une charge au repos :

la charge q placée en 0, crée au point M les champs E et B suivants :

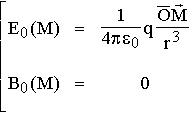
une charge mobile crée dans l'espace qui l'entoure un champ électrique identique à celui qu'elle créerait si elle était au repos et un champ magnétique qui dépend de sa vitesse. En effet, le principe de relativité impose que l'on ne puisse pas discerner si on se déplace par raport à la charge ou si la charge se déplace par rapport à nous. Il faut donc qu'une charge en déplacement créé un champ magnétique qui puisse expliquer la force que l'on subirait si l'on se déplaçait dans le champ de la charge immobile.

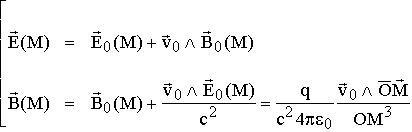
B est en fait une manière simple de décrire l'action du champ électrique par un changement de référentiel.

on définit la constante m₀, telle que : m₀ = 1/ e₀ c²

En généralisant la formule ci dessus, on trouve la Loi de Biot et Savart :

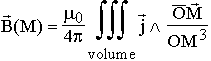
où j est la densité de courant (la somme des charges q multipliées par leur vitesse v)

a) cas d'un circuit filiforme

On considère un circuit fermé parcouru par un courant I constant, circulant dans un fil dont le diamètre est négligeable devant toutes les autres dimensions du problème. On cherche à determiner le champ magnétique B(M) créé par ce courant en un point M de l'espace.

Soit P un point du fil, et dl un élément du fil contenant P

La Loi de Biot et Savart indique que le champ magnétique créé au point M par le courant I circulant dans le circuit (c) est donné par l'intégrale :

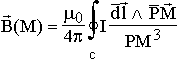
b) cas d'un fil rectiligne infini

on considère que l'on a un fil rectiligne infini (en fait très long) dont la circuit est bouclé à une distance très grande devant celle à laquelle on veut calculer le champ. La contribution de la boucle à l'intégrale de Biot et savart sera donc négligeable devant la contribution de la partie rectiligne.

la contribution du petit élément dl donne le champ dB :

c'est une contribution perpendiculaire au plan de la figure. Pour obtenir le champ total on doit faire la somme le long du fil de ces contributions en tenant compte du facteur géométrique (dl _^ r)/r³ qui varie quand on se promène sur le fil, c'est à dire quand on fait l'intégrale avec z qui varie de - µ à +µ .

On a les relations suivantes : sinq = d/r et tgq = - d/z

qui donnent : r = d/ sinq et z = - d/ tgq

la deuxième expression donne : dz/dq = d . 1/tg²q . d(tgq)/dq

= d/tg²q .1/cos²q

soit finalement : dz = d.dq/sin²q

On peut donc réécrire le terme géométrique uniquement en fonction de q de la manière suivante :

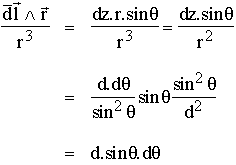
on a alors :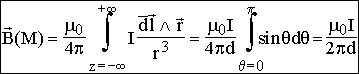

6/ Loi d'Ampère rot B = m₀j

Dans le cas d'un champ vectoriel à divergence nulle (ce qui est le cas du champ magnétique B), on peut écrire le champ B comme étant le rotationnel d'un autre champ A que l'on nomme potentiel vecteur. On a alors :

B = rot A

On peut alors montrer que le potentiel vecteur verifie la relation :

DA+ m₀j = 0

comme rot(rot (A)) = grad(div(A))-Laplacien(A) et que div(A) =0, on obtient facilement : rot(rot(A)) = - Laplacien(A)

et donc : rot(B) = m₀j qui est la loi d'Ampère

sous forme intégrale, cette loi s'écrit :

Ou encore : la circulation de B sur une courbe fermée est proportionnelle à l'intensité totale traversant la surface intérieure du contour c.

Ici on voit la relation profonde qui existe entre courant j et champ magnétique B. La forme spatiale du champ fabrique du courant ou inversement : à chaque courant est associé un champ en rotationnel...

7/ les phénomènes dépendant du temps

a) La conservationde la quantité d'electricité implique (en phénomène stationnaire) :

si des charges sont crées (ou annihilées) au cours du temps pour compenser une divergence non nulle, alors cette relation devient :

où r est la quantité de charges et dr/dt le taux de création de ces charges au cours du temps.

b) équations sur E

On peut comme d'habitude écrire que le champ electrostatique E dérive d'un potentiel V :

En phénomènes dépendant du temps, l'équation doit être complétée d'un terme qui provient de l'existance du champ magnétique induit. on a alors :

qui donne aisément :

(1)

On a également le théorème de Gauss qui reste valable :

(2)

c) équations sur B

le théorème d'Ampère généralisé devient :

(3)

et encore B=rot(A) qui donne :

(4)

l'ensemble de ces 4 équations constitue les équations de Maxwell.