CHAMP MAGNETIQUE TERRESTRE

1/ Historique

fig 2.1 page 16

les éléments principaux du champ magnétique :

- la déclinaison D est la déviation de l’aiguille de la boussole par rapport au Nord géographique.

- l’inclinaison I est l’angle entre le champ total et sa composante horizontale (l’inclinaison de l’aiguille de la boussole vers le haut ou vers le bas). Elle est comptée positive vers le bas.

Les composantes horizontales (X et Y) et verticale (Z) du champ total (F) sont donc données par :

Z = F sin (I)

Y = F (I) sin(D)

X = F cos(I) cos(D)

Les propriétés attractives de certains minéraux (magnétite) sont connues depuis les anciens grecs (Thalès - 6^ème siècle AC) et les vieux chinois (du 3^ème siècle AC - 6^ème siècle PM). En chinois, on nommait ces minéraux "tzhu shih" c'est à dire "pierres-qui-s'aiment" (aimants).

- la première boussole (cuillère de Wang Chen-to) date du premier siècle avant JC.

- Les boussoles arrivent en Europe vers le 12^eme siècle (Alexandre Neckham, moine de St Albans, 1190). A cette époque on imagine que l'aiguille de la boussole pointe vers l'étoile polaire, puis qu'il existe une montagne de magnétite polaire qui attire toutes les aiguilles.

- Roger Bacon (1266) puis Petrus Peregrinus (Epistola de magnete - 1269) remettent cette idée en cause. Ce dernier se livre à des expériences avec des aimants de forme sphérique. Il découvre le concept de pôles, la nature dipolaire des aimants et formule la loi selon laquelle les pôles identiques se repoussent et les pôles opposés s'attirent. Il décrit le premier "compas" à aiguille flottante.

- au début du 15^ème siècle, on redécouvre en Europe la déclinaison, connue en chine depuis la première mesure de I-Hsing (moine Bouddhiste) en 720. Les premières mesures cataloguées sont établies par Georg Hartmann, vicaire de Nurenberg, à Rome en 1510.

- le même Hartmann découvre l'inclinaison en 1544 mais sa découverte reste inconnue (jusque en 1813). C'est Robert Norman (Hydrographe Anglais) qui la redécouvre en 1576.

- de 1538 à 1541, João de Castro (commandant l'un des 11 navires de l'expédition portugaise vers les Indes) effectue 43 mesures de la déclinaison tout au long de son voyage et découvre que celle ci varie en fonction de la position.

(de Castro mesure 2 fois l'azimut du soleil, avant et après midi pour deux élévations identiques (déterminées avec un cadran solaire). La différence entre les deux mesures est la déclinaison)

- en 1546, Gerhard Mercator, mathématicien et géographe, démontre à partir des mesures de déclinaison que l'endroit vers lequel pointe l'aiguille aimantée ne peut se trouver "dans les cieux" mais bien sur la Terre !

- enfin, en 1600, William Gilbert (docteur de la reine Elisabeth I) reprend les expériences de Peregrinus, et grâce aux nouvelles connaissances (l'existence de l'inclinaison) écrit dans son célèbre traité "de magnete" :

Magnus magnes ipse est globus terrestris

C'est la première propriété attribuée globalement à la Terre (87 ans avant la gravitation de Newton)

- en 1634, Henry Gellibrand, Astronome au Gresham College, découvre sur la base de ses mesures et de mesures plus anciennes que la déclinaison change avec le temps. Il attribue cette observation à l'imprécision des mesures anciennes sans imaginer que le champ varie vraiment !

date	observateur	déclinaison
16 Oct. 1580	William Borough	11.3° E
13 Juin 1622	Edmund Gunter	6.0° E
16 Juin 1634	Henry Gellibrand	4.1° E

fig 1.3 page 5

- la première carte de déclinaison est publiée en 1702 par Edmund Halley après deux voyages à but uniquement scientifique (les premiers) en 1698 et 1700 dans l'Atlantique Nord et Sud.

- la première carte d'inclinaison est publiée à Stockholm par Johann Carl Wilcke en 1768.

- entre 1799 et 1803, Alexandre von Humboldt découvre que l’intensité du champ magnétique varie avec la latitude.

Au cours de ces voyages aux Amériques, il fait "vibrer" l'aiguille de sa boussole et compte le nombre d'oscillations sur une période de 10 minutes. Le nombre d'oscillations sur l'équateur magnétique au Pérou est de 211 et décroît symétriquement vers le Nord et vers le Sud, indiquant une augmentation de l'intensité du champ magnétique vers les pôles.

- les premières cartes d'intensité sont publiées en 1825 et 1826 par Christopher Hansteen, professeur de Mathématiques appliquées a Oslo.

- en 1838, Carl Friedrich Gauss calcule les premiers coefficients du développement du champ en harmoniques sphériques (à la main). Il utilise pour cela des mesures en 84 endroits espacés de 30° en longitude sur 7 parallèles. Il en déduit la position des pôles magnétiques (donnée par l'axe du dipôle dans son développement).

- James Ross "découvre" le pôle Nord magnétique en 1831 (70°05'N, 96°46'W)

- l'expédition Shackleton (David et Mawson) "découvre" le pôle Sud magnétique en 1909 (et se trompe de 130 km).

2/ La mesure du champ magnétique

3/ Le champ magnétique interne

a) harmoniques sphériques

Comme d'habitude, on montre que le champ dérive d'un potentiel :

et que ce potentiel vérifie l'équation de Laplace :

Y est un champ scalaire que l'on peut donc exprimer simplement sur la base des harmoniques sphériques :

Ou encore (en fonction des champs sphéroidal, poloidal et toroidal) :

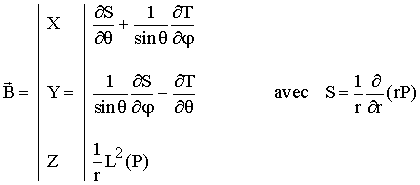
b) relation avec le courant électrique

la loi d'Ampère (simplifiée) s'écrit :

et le champ lui même s'écrit :

On obtient donc :

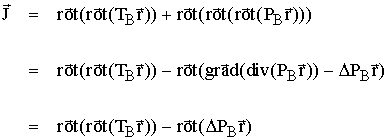
Or, J lui même s'écrit sous la forme :

on obtient donc finalement, la propriété simple suivante :

c) expression des premiers termes du développement du potentiel Y

Tableau des valeurs numériques des premiers coefficients (de degré l=1)

l	m	a_l^m (en nT)	b_l^m(en nT)
1	0	-30 001	0
1	1	-1950	5634
2	0	-2038	0
2	1	3035	-2134
2	2	1652	-179
3	0	1293	0
3	1	-2156	-38
3	2	1244	261
3	3	851	-235

le premier terme du développement (Y₁⁰) est donné par :

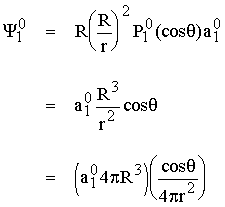
qui est tout simplement le potentiel associé à un dipôle d'intensité (I=a₁⁰ 4pR³) orienté selon l'axe Z (vertical). L'amplitude de a₁⁰ est donc linéairement reliée à l'intensité du dipôle axial terrestre(qui pointe vers le bas car a₁⁰ est négatif).

De même, le terme (Y₁¹) est donné, d'une part par a₁¹, et d'autre part par b₁¹. Le terme en a₁¹ donne :

si g est l'angle entre les axes x et r, il est facile de montrer que cosg = cosj sinq. Du coup le terme en a₁¹ apparaît comme la contribution d'un dipôle orienté selon l'axe horizontal x.

de manière similaire, le terme en b₁¹ donne :

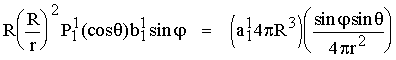
qui correspond à un dipôle orienté selon le deuxième axe horizontal y.

Le dipôle total p, peut donc être simplement déterminé par la somme vectorielle de ces trois dipôles. On obtient alors pour l'amplitude de p:

avec les valeurs numériques indiquées dans le tableau, on trouve un dipôle incliné d'environ 11,5° par rapport à l'axe de rotation de la Terre. A peu près 90% du champ magnétique terrestre en surface peut être expliqué par ce dipôle comme le montre le spectre.

Figure du spectre

La courbe en points blancs montre le champ tel qu'il est mesuré à la surface de la Terre avec une nette rupture de pente vers le degré 14. Les termes de degré inférieur à 14 sont attribués à des sources profondes (le Noyau), les autres termes à des sources superficielles (la croûte).

La courbe en points noirs montre le champ extrapolé à la surface du noyau. On voit que les termes de degré inférieur à 14 s'alignent alors sur une droite qui a sensiblement la même pente que celle de l'énergie des termes en provenance de la croûte, mesuré à la surface. Les termes de degré supérieur à 14 divergent, preuve supplémentaire qu'ils sont extérieurs à la surface noyau-manteau...

d) Unicité de la source et problèmes

Attention ! Encore une fois, un coefficient seul de la décomposition en harmonique sphérique n'a pas forcémént de sens physique "réel". Par exemple, si on analyse la contribution au champ d'un dipôle décalé du centre de la Terre d'une distance d suivant l'axe z.

placé au centre de la Terre, il serait représenté par :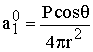

décalé, il donne :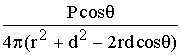

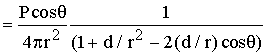
comme d << r, on peut faire un développement de Taylor : (1+x)^-1 ~ 1-x

et on obtient :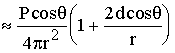

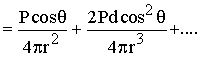
Ce qui veut dire qu'un dipôle décalé de d peut être représenté par un dipôle centré (de même intensité) plus un quadrupôle augmenté de 2d, plus un octupôle, etc...

Cela montre qu'un dipôle décalé dans le noyau est mathématiquement indiscernable d'un dipôle centré associé à une série de termes de plus haut degrés (il n'y a pas unicité de la décomposition en harmonique sphérique).

D'autre part, cela montre que chaque coefficient ne représente pas la contribution de sources magnétiques distinctes et n'a pas de sens physique particulier.

4/ Variations temporelles du champ

Depuis les premières mesures de Gellibrand (1635) on sait que le champ magnétique varie : A Londres la déclinaison passe de 11°E en 1576 à 24°W en 1823 avant de revenir vers les 5°W d'aujourd'hui.

fig 2.7 page 39

variation de la déclinaison à Londres (Angleterre) et Hobart (Tasmanie)

En fait, les variations du champ magnétique terrestre se produisent à toutes les échelles et surtout avec des périodes allant de la milliseconde aux millions d'années.

Phénomène	période	amplitude (nT)
Micropulsations	1ms-3mn	£ 1
variation solaire (jours calmes) (S_q)	24h	~ 20
variation solaire (jours agités) (S_d)	24h	~ 5-20
variation lunaire (L)	25h	~ 1
agitation magnétosphérique	1h-2h	~ 10
tempêtes magnétosphériques
(a) phase initiale	~4h	~ 15
(b) phase principale	~8h	~ 35
(c) phase de récupération	~60h	~ 35
champ magnétique externe	£ 4 ans
champ magnétique interne	> 4 ans
cycle des taches solaires	11 et 22 ans
dérive vers l'Ouest	2000 ans
inversion	10⁵ - 10⁸ ans

En général, on attribue les perturbations qui ont une période inférieure à un an au champ externe et celles qui ont une période supérieure à un an au champ interne.

Cela ne veut pas dire qu'il n'y a pas de perturbations à courte période dans le noyau mais qu'elles ne sont pas visibles à la surface. En effet, le manteau étant électriquement conducteur, il agit comme un "écran" magnétique qui empèche les perturbations à hautes fréquences de "passer" à travers.

Le théorème d'Ampère généralisé (rot B=m₀J + e₀ m₀ dE/dt) peut s'écrire sous la forme :

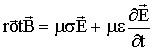
où s est la conductivité électrique du manteau.

En prenant le rotationnel de cette équation, on obtient :

En utilisant une autre équation de Maxwell (rot E = -dB/dt), on obtient :

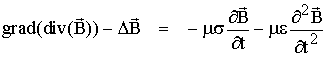
soit enfin :

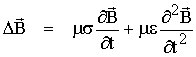
cette équation est dite "équation d'onde" de B. le premier terme de droite représente un terme d'amortissement. En effet, la solution de cette équation est du type :

où k₁ et k₂ sont les parties réelles et imaginaires du nombre d'onde k, et w est la fréquence. En substituant cette expression de B dans l'équation, on montre que ça marche pour des valeurs définies de k₁ et k₂ en fonction de e,m,s, et w. Donc B devient nul à partir d'une certaine distance x, définie pour un w donné (e,m,s étant ceux du manteau terrestre). Avec les valeurs numériques classiques, on trouve de l'ordre de 1 pulsation par an comme fréquence de "coupure".

5/ paléomagnétisme

a) enregistrement du champ ambiant dans les minéraux

La plupart des minéraux contiennent des "éléments" magnétiques, c'est à dire des "grains" composés d'alliages ou d'oxydes qui sont sensibles au champ magnétique ambiant. De ce fait, quand une roche se forme, elle acquière une magnétisation parallèle au champ magnétique ambiant qui existe au moment où elle se forme.

Deux "grains" qui ont chacun leur moment magnétique propre, vont vouloir s'aligner entre eux. Ces ajustements demandent de l'énergie et ne sont donc possibles que si la température de la roche est suffisamment élevée.

La température seuil en dessous de laquelle les ajustements ne sont pas possible est la température de Curie. Elle est différente pour chaque minéral.

En général, les roches sont fabriquées à chaud. Le processus est alors le suivant:

chaleur	=	énergie thermique

	=	désordre atomique

	=	désordre magnétique

imposition d'un champ extérieur	=>	alignement des moments sur ce champ


refroidissement < temp. De Curie	=>	l'orientation est figée

	=	Magnétisation Thermo Remanente (TRM)

C'est typiquement ce qui se passe dans une coulée de lave, ou dans une poterie ancienne.

Dans les sédiments, le processus est différent, ce sont des grains déjà magnétisés qui vont se déposer en s'orientant selon le champ magnétique ambiant au moment de leur dépot

Bien évidemment, la magnétisation primaire peut être suivie d'une remagnétisation totale ou partielle du minéral. Cela rend l'analyse plus compliquée qu'il n'y parait !

Les minéraux magnétiques les plus courants sont de deux types :

- antiferromagnétique (si les moments magnétiques adjacents sont d'égale amplitude)

- ferromagnétique (si les moments magnétiques adjacents ne sont pas d'égale amplitude)

certains minéraux à base de mélange d'Hématite (Fe₂O₃) et d'Ilménite (FeTiO₃) (10% - 90%) sont globalement antiferromagnétique avec des agrégats ferromagnétiques

table 3.3 p 72

b) la dérive du dipôle

Les techniques de paléomagnétisme permettent donc de mesurer ce qu'était le champ magnétique à telle ou telle époque et à tel ou tel endroit. Pour ce faire, il suffit de prélever un échantillon de roche en l'orientant dans l'espace, de le dater, puis de mesurer son aimentation rémanente. Ensuite, en supposant que le champ de l'époque était dipôlaire, on calcule l'orientation de ce dipôle par simple reconstruction en trigonométrie sphérique.

on obtient la position du paléo-pôle (l¹,f¹) à partir de la position du site (l,f) et du champ "enregistré" dans l'échantillon par les formules suivantes :

sin l¹ = sinl cosq + cosl sinq cosD

f¹ = f + b où b est donné par : sinb = sinq sinD / cos l¹

fig 3.7 p 81

en compilant les mesures effectuées pour les derniers 2000 ans (sur le mêm continent), on trouve que le pôle magnétique s'est significativement déplacé au cours de cette période.

fig 4.4 p 101

en comparent les mesures pour les derniers 350 million d'années en Europe d'une part et en Amérique d'autre part, on trouve des "chemins" différents pour le pôle magnétique.

fig 3.8 p 83

En fait, cette différence n'est qu'apparente, et vient du fait que les continents eux mêmes se sont déplacés l'un par rapport à l'autre de manière significative pendant ces derniers 350 Ma.

Si on tient compte de l'ouverture de l'Atlantique, alors les deux trajets du pole Nord magnétique coïncident de nouveaux. C'est une preuve de plus de la tectonique des plaques.

c) dérive vers l'ouest du champ dipôlaire

En analysant les chemins du pôle sur une certane période de temps à un site donné, on trouve une tendance à une rotation horaire, ou anti-horaire suivant les cas.

fig4.13 p 117

Cette rotation, est assimilée à la dérive vers l'ouest du champ total par Runcorn en 1959.

fig4.12 p 115

On imagine donc que la dérive vers l'ouest constaté dans le champ global peut être due au déplacement d'une source magnétique dans le noyau (par exemple un dipôle).

d) excursions du dipôle

Toujours en analysant les données paléomagnétiques, on trouve dans certains enregistrement une variation extremement rapide de la position du pôle dans le temps. ces enregistrements sont rares car il faut soit un volcan qui produise des coulées de lave très régulièrement pendant plusieurs milliers d'années, soit un lac dans lequel la sédimentation se fait très rapidement.

fig 4.15 p 124

On voit que non seulement la déclinaison est instable, mais surtout que l'inclinaison change de signe autour de 25 000 ans. Le dipôle s'est donc retourné pendant un temps assez court avant de revenir en position normale.

Par ailleurs, l'amplitude du champ est considérablement réduite pendant cette période, ce qui indique un phènomène complexe. En effet, il y a 3 explications possibles à cette excursions :

- le dipôle a vraiment changé d'axe

- la partie dipolaire du champ a diminué brusquement et c'est la partie non dipolaire qui a dominé le champ global pendant un certain temps (ce qui infirme l'hypothèse de départ qui permet de calculer ce chemin du dipole)

- Une source magnétique intense est brusquement apparue avant de disparaitre au bout d'un laps de temps assez court.

Les deux premières hypothèses imposent un phénomène global, ce qui pose un problème d'énergie. d'autre part, on devrait voir la même séquence en d'autres endroits à la même époque, ce qui n'est pas le cas.

la troisième hypothèse n'implique qu'un phénomène local. En effet, un petit dipôle placé n'importe où dans le noyau peut donner un champ non dipolaire très localisé en surface (15° soit environ 1500 km).

e) inversions du champ

En étudiant les enregistrements paléo magnétiques sur des périodes toujours plus longues, on trouve des séquences pour lesquelles le dipôle pointe vers le haut (pôle Nord) et d'autres ou il pointe vers le bas (pôle Sud).

C'est ce que l'on appelle des inversions.

fig5.9 p 152

si on regarde sur une période de temps plus courte, on retrouve le même schéma.

fig 5.3 p 140

fig 5.4 p 141

(réduction)

Bien quelles se produisent de manière apparament chaotique, ces inversion ne se produisent pas tout à fait indépendamment les unes des autres.

une analyse en série de Fourier montre qu'il n'y a pas de fréquence préférencielle pour les inversions (contrairement au Soleil qui s'inverse tout les 11 ans)

Cependant, les périodes de polarités normales ou inverses ont des durées qui ne sont pas uniformément réparties dans le spectre. Les périodes de polarité donnée sont de plus en plus courte ce qui laisse à penser qu'il y a une corrélation entre les époques successives.

fig 5.11 p 157

l'étude de ces séries temporelles a suscité la théorie du chaos et des attracteurs étranges dans les années 30 et 40. A l'heure actuelle, on n'est toujours pas capable de modéliser précisement ce qui se passe lors d'une inversion, ni pourquoi une inversion a lieu.

le principal problème est d'imaginer le mécanisme qui "relance la dynamo" très rapidement (l'intensité du champ descend très bas puis remonte à son niveau initial après l'inversion).