1/
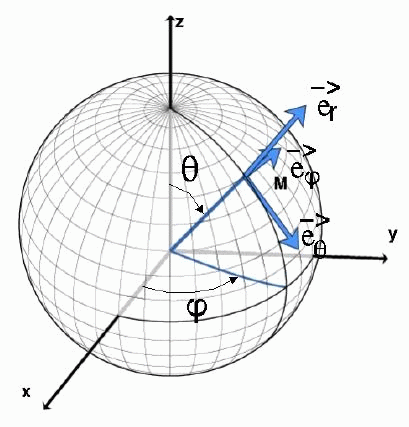
Opérateurs classiques en coordonnées sphériques

gradient :
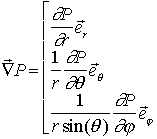
divergence :![]()
rotationnel :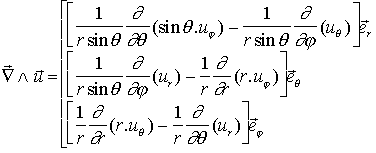
Laplacien :
![]()
où
L2, dit Laplacien angulaire, vaut :
![]()
2/ harmoniques
sphériques
![]()
![]()
|
l = 1 m = -1 |
l = 1 m = 0 |
l = 1 m = 1 |
|||||||||
|
|
|||||||||||
|
l = 2 m = 0 |
l = 2 m = 1 |
l = 2 m = 2 |
|||||||||
|
|
|||||||||||
|
l = 36 m = 0 |
l = 36 m = 12 |
l = 36 m = 24 |
l = 36 m = 36 |
||||||||
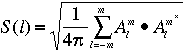
d)
Corrélation entre deux champs
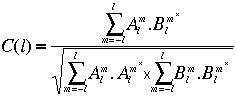
|
|
|
|
|
|
|
Application à la topographie terrestre
|
|
|||||||||
|
Les premiers coefficients de la décomposition de la topographie terrestre en harmoniques sphériques |
|||||||||
|
Décompositions de la topographie terrestre degré par degré, de 0 à 6 |
|||||||||
|
l |
m |
alm |
blm |
||||||
|
0 |
0 |
-8152 |
0 |
||||||
|
1 |
0 |
2265 |
0 |
||||||
|
1 |
1 |
-1481 |
1025 |
||||||
|
2 |
0 |
1825 |
0 |
||||||
|
2 |
1 |
-842 |
764 |
||||||
|
Reconstitutions de la topographie terrestre du degré 0 jusqu'à un degré à chaque fois plus élevé (6, 16, puis 36). Plus on va loin, plus la "qualité" de la représentation est bonne. |
|||||||||
|
2 |
2 |
-1039 |
201 |
||||||
|
3 |
0 |
-616 |
0 |
||||||
|
3 |
1 |
336 |
287 |
||||||
|
3 |
2 |
-1115 |
-1145 |
||||||
|
3 |
3 |
-290 |
1363 |
||||||
|
4 |
0 |
1316 |
0 |
||||||
|
|
|
|
|
||||||
|
|
|||||||||
|
|
|
|
|
||||||
|
|
|
||||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||