THEORIE MATHEMATIQUE DU REBOND POST-GLACIAIRE
Isostasie. Cas général et formalisme.
La prédiction de déformations de la Terre solide associées à une
charge posée à la surface est un problème classique de géophysique
(voir par exemple Farrell, 1972. Comme, depuis les années 1980, et surtout
1990, le développement des techniques de positionnement spatiales telles
que SLR, VLBI et GPS a permis des mesures de positions et vitesses de points
situés à la surface de la Terre avec une précision de plus en plus
grande (autour de 1 mm pour le VLBI), les prédictions de réponse de la
surface terrestre à des effets de charge doivent également se faire
de plus en plus précises. Il importe en effet de pouvoir incorporer
des modèles de mouvements verticaux dans les inversions de positions
et vitesses des sites GPS ou VLBI, et ce avec une précision suffisante.
Cela concerne aussi bien les réponses à la pression atmosphérique
(vanDam, 1987) à une surcharge océanique (Scherneck, 1991),
ou aux effets visco-élastiques de la déglaciation du Pleistocène
(Tushingham, 1991). Dans la suite, nous présentons de façon
progressive le formalisme utilisé dans la plupart des modélisations
récentes de rebond post-glaciaire (fonctions de Green et décomposition
en harmoniques sphériques). On considérera différents cas de comportement
du manteau supérieur, selon une rhéologie élastique, et visco-élastique
respectivement.
D'après Farrell, 1972, cette approche consiste dans un premier temps
à calculer les fonctions de Green pour les déplacements radial et
tangentiel associés au potentiel de marée et à une charge sur
une Terre à symétrie sphérique
ayant une rhéologie pûrement élastique. On sait depuis longtemps
que le comportement du manteau est assez éloigné de celui d'un
solide élastique (viscosité comprise entre 1020
et 1023 Pas approximativement), mais pour un
effet de charge ayant une constante de
temps suffisamment brève (de la semaine à quelques dizaines
d'années), l'approximation élastique peut suffire à modéliser
la réponse en surface avec une exactitude satisfaisante.
Dans tous les calculs de réponse terrestre à une sollicitation
externe, on doit en fait tenir compte de deux effets agissant sur
la surface et le potentiel de gravitation : celui dû au potentiel
de marée et celui dû à la charge en elle-même.
On commence par l'exposé de cet effet de marée terrestre, qui sera
ensuite incorporé aux calculs globaux.
La réponse du modèle de Terre à une charge massique
arbitraire posée à la surface peut ensuite être calculée par le biais
d'un produit de convolution en surface avec la fonction de Green appropriée.
En pratique, la fonction de Green est discrétisée sur l'ensemble
de la surface de la Terre, sous forme d'éléments finis, la taille
de la surface élémentaire étant conditionnée par la résolution
de la charge appliquée.
Le formalisme spectral se fonde sur les nombres de Love Love, 1909.
Ces nombres gouvernent la réponse d'un modèle planétaire à un
forçage de potentiel gravitationnel ou de charge en surface, respectivement.
Les nombres de Love HL,
LL, et
KLreprésentent
le coefficient d'harmoniques sphériques de degré L
des déplacements radial et tangentiel, et de la perturbation du potentiel de gravitation
dûs à la redistribution de masse (marées terrestres) provoquée par
le potentiel de marée. Si l'on désigne par
W( ,
,
 ,t).
Ce potentiel de marée terrestre au point de la surface terrestre
de latitude
,t).
Ce potentiel de marée terrestre au point de la surface terrestre
de latitude  , de longitude
, de longitude
 et à l'instant t,
la réponse de la Terre à ce potentiel s'écrira :
et à l'instant t,
la réponse de la Terre à ce potentiel s'écrira :
U =
où YLm( ,
,  )
correspond aux harmoniques sphériques normalisées sur la surface de la Terre, et
où le symbole
)
correspond aux harmoniques sphériques normalisées sur la surface de la Terre, et
où le symbole  désigne l'opérateur
gradient à deux dimensions, soit :
désigne l'opérateur
gradient à deux dimensions, soit :
 =
=
Dans ce cas, les nombres de Love s'écrivent
HL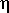 ,
LL
,
LL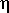 et
KL
et
KL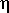 ,
où
,
où 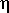 fait référence à
la rhéologie élastique adoptée, et L
au degré de la décomposition en harmoniques
sphériques, et désignent, respectivement, les coefficients d'harmoniques
sphériques des déplacements radial et tangentiel, et de la perturbation
gravitationnelle provoqués par la charge.
fait référence à
la rhéologie élastique adoptée, et L
au degré de la décomposition en harmoniques
sphériques, et désignent, respectivement, les coefficients d'harmoniques
sphériques des déplacements radial et tangentiel, et de la perturbation
gravitationnelle provoqués par la charge.
Les fonctions de Green correspondant à cet effet de charge s'écrivent :
G =
P =
respectivement, où a désigne le rayon moyen de la Terre, M sa masse,
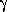 est un vecteur unitaire tangent à
la surface, selon le grand
cercle qui passe par le point de charge
(
est un vecteur unitaire tangent à
la surface, selon le grand
cercle qui passe par le point de charge
( ',
',
 ')
vers le point d'observation
(
')
vers le point d'observation
( ,
,  ), et
), et
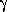 désigne la distance angulaire entre
les deux points.
désigne la distance angulaire entre
les deux points.
Notons que 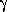 peut être donnée par :
peut être donnée par :
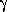 = cos
= cos cos
cos ' + sin
' + sin sin
sin ' cos(
' cos( -
- ')
')
Enfin, PL représente la polynôme de
Legendre de degré L.
Dans le cas particulier élastique, si l'on désigne par
G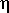 (
(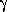 )
une fonction de Green, la réponse de la Terre à une masse surfacique
appliquée au point (
)
une fonction de Green, la réponse de la Terre à une masse surfacique
appliquée au point ( ',
',
 ') et au temps t
sera donnée par :
') et au temps t
sera donnée par :
R =
G =
où d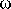 désigne la surface élémentaire autour du point (
désigne la surface élémentaire autour du point (
 ',
',
 ').
').
La réponse R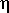 (
( ,
, ,t)
sera donc une quantité scalaire pour les
fonctions de Green radiale et de potentiel, et
un vecteur pour la réponse tangentielle correspondant à la fonction.
,t)
sera donc une quantité scalaire pour les
fonctions de Green radiale et de potentiel, et
un vecteur pour la réponse tangentielle correspondant à la fonction.
En appliquant directement les équations précédentes, et à condition
de discrétiser suffisamment la charge, puis de
procéder à l'intégration par éléments finis, on obtient la
réponse de la Terre (e.g. (Jentzsch, 1985).
Dans le cas de déformations de la surface associées à l'effet de charge
du rebond post-glaciaire, l'approximation élastique est insuffisante. Du fait
des constantes de temps, longues, associées au comportement d'une calotte
de glace, les nombres de Love correspondants deviennent dépendant
du temps. D'après le principe de correspondance (Biot, 1954),
on peut les écrire sous la forme :
Le formalisme explicité par exemple par (Peltier, 1985) permet de calculer
les amplitudes de mode normal et les temps de relaxation correspondant aux pulsations
propres.
On écrit ensuite de la même façon que dans le cas pûrement
élastique les fonctions de Green associées :
L'intégration de la réponse sur l'ensemble de la surface terrestre se fait
de la même façon que dans l'équation ?, à ceci près que la
fonction de Green dépend du temps et qu'il faut distinguer
le temps t' auquel s'applique la charge surfacique
du temps t d'observation. L'intégration devient un
double produit de convolution sur la surface de la Terre et le temps, soit :
La charge est discrétisée, en général sous
forme de disques d'épaisseur constante, avant intégration. Cette méthode,
incluant la prise en compte de la redistribution océanique, ainsi que
les conséquences de la déformation crustale, a été utilisée
à maintes reprises (par exemple (Wu et Peltier, 1983;
James et Morgan 1990, ou Spada et al., 1992)
Cette méthode, reprenant le formalisme de base exposé précédemment,
a été exposée par Mitrovica et al., 1994a. Elle s'applique
dans le cas d'un modèle de Terre à symétrie sphérique, et
consiste à décomposer la charge en surface
selon les harmoniques sphériques, plutôt que de la discrétiser,
soit :
Si l'on reprend les fonctions de Green de l'équation ? et la réponse terrestre
de l'équation ?, on va obtenir par exemple pour la réponse en déplacement
tangentiel :
Comme et que l'opérateur
ne s'applique qu'aux quantités , et comme ,
on peut écrire :
Ceci compte tenu de l'orthonormalisation des harmoniques sphériques. De la
même façon, on aura :
pour le déplacement radial à la surface de la Terre, et :
pour l'effet sur le potentiel de gravité.
L'énorme avantage de cette décomposition de la charge
en harmoniques sphériques est que cela permet d'adapter la résolution
spatiale du calcul par simple troncature du degré maximal de décomposition.
Cette stratégie se révèle particulièrement payante lorsque la résolution
de la charge varie spatialement, ou encore lorsqu'on reprend un calcul déjà
effectué, avec un modèle de charge amélioré, dont la résolution
s'est affinée.
Dans la pratique, la charge peut être constituée
d'une charge atmosphérique, océanique, ou d'une surcharge glaciaire,
ou encore une combinaison de plusieurs de ces éléments.
En reprenant la décomposition de la charge, la réponse
locale de la Terre, prenant en compte aussi bien l'effet de marée
terrestre que l'effet de charge, s'écrit :
et
où le vecteur est défini par :
On a considéré jusqu' à présent que les nombres de Love, qu'ils
s'appliquent au potentiel de marée ou à l'effet de charge, sont
indépendants de la fréquence.
On sait que ce n'est pas le cas, et qu'il faudrait écrire :
Il faut ensuite introduire les expressions explicites du potentiel de
marée et de l'effet de charge.
Le potentiel de marée est exprimé sous forme d'une somme de termes
sinusoïdaux, soit pour le terme de degré L et
d'ordre m :
où , et représentent la fréquence, la phase et l'amplitude du
nème composants sur un total
de nm. De la même façon :
et on a au total les expressions :
et
Il faut remarquer que ce formalisme n'est pas adapté à tous les cas de charge. Par
exemple, pour la réponse à la fonte actuelle des calottes et des glaciers, qui
a des constantes de temps très longues, on peut considérer que les nombres de Love
sont indépendants de la fréquence.
Les équations ?, ? et fournissent le système
permettant d'obtenir la réponse à l'effet de charge compte tenu des
modifications du potentiel de perturbation gravitationnel.
La perturbation du potentiel de gravitation total peut se décomposer
en harmoniques sphériques :
où chaque terme inclut la réponse au potentiel
de marée, la charge de l'océan et
la charge autre que celle de l'océan (par exemple
l'allègement de la charge glaciaire).
On définit la fonction océan, , comme égale à l'unité
aux endroits recouverts par la mer, nulle partout ailleurs (soit
les composantes de sa décomposition en harmoniques sphériques). On désigne
par ? l'épaisseur de l'eau dans l'océam , ?
les composantes associées, et ?,
où 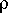 w est la densité de l'eau de
mer.
w est la densité de l'eau de
mer.
L'équation qui gouverne la hauteur d'eau dans les océans s'écrit au total :
Physiquement, elle reflète le fait que la charge océanique perturbe le champ
de gravité, qui a son tour vient perturber l'équilibre océanique. L'expression
pour la quantité ? peut être obtenue en imposant une contrainte
de conservation de la masse sur l'ensemble de l'océan.
En intégrant ? la surface ?, en utilisant le fait que , on obtient :
et
est obtenu par conservation de masse, en fonction des autres effets de charge.
On considère la redistribution océanique résultant de la fonte des
glaciers et calottes. On a alors :
et
où 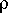 i est la densité de la
glace et où .
est la composante de degré L, et d'ordre
m de l'épaisseur
de la glace.
Pour la redistribution océanique, une première approximation est donnée
par la redistribution eustatique :
i est la densité de la
glace et où .
est la composante de degré L, et d'ordre
m de l'épaisseur
de la glace.
Pour la redistribution océanique, une première approximation est donnée
par la redistribution eustatique :
qui se place dans le cas d'une redistribution de l'eau de fonte d'une manière
indépendante de la géographie.
Dans le cas de cette variation, séculaire, on calcule la réponse globalement plutôt
que pour une fréquence spécifique.
On se place à nouveau dans le cas d'une Terre sphérique avec une rhéologie
mantellique visco-élastique. Les équations ?, ?, et ?, mènent à :
et
avec
Le premier terme du membre de droite de représente la composante
élastique de la réponse, le terme suivant la composante non-élastique.
Si on applique cette méthode à la déglaciation du Pléistocène (fonte des
grandes calottes de l'hémisphère Nord et d'une partie de l'Antarctique), on
représente généralement la décroissance de ces calottes au cours du temps
comme une succession de paliers. Cette modélisation n'entraîne pas de perte
de généralité dans la mesure où les intervalles de temps peuvent être
aussi petits qu'on le désire. En appliquant la même discrétisation à la
charge en surface, on peut écrire :
où H représente la fonction de Heaviside et
N le nombre total d'incréments.
On a alors :
En réinjectant ces quantités dans les équations ? et ? on obtient :
et
Les sommes sur n incluent tous les éléments de charge dont le début se situe
avant le temps d'observation t. N(t) représente donc le nombre d'incréments sur un
total de N, qui satisfont ?.
De façon générale, on peut séparer les effets de charges provenant de la
redistribution océanique, des autres effets, dits résiduels. On peut donc écrire :
et
où les Ylm sont les coefficients de
la décomposition en harmoniques sphériques de la hauteur d'eau dans l'océan
à léquilibre, et les ?
les coefficients associés pour le changement incrémental.
On utilise les expressions précédentes de ? et ? avec la décomposition
de la charge exprimée ci-dessus.
Dans ce cas particulier, le terme résiduel concerne l'épaisseur de glace, soit :
et
où Ylm représentent les coefficients d'harmoniques sphériques
de la charge glaciaire, et ? les changements incrémentaux associés
pour le pas de déglaciation.
Le développement de modèles de rebond à partir d'une Terre
présentant une structure visco-élastique stratifiée a permis de montrer
que, contrairement à
l'idée longtemps admise, la déglaciation continue à produire des effets
sur la dérive du pôle longtemps après que la variation de masses ait
cessé. La quantité 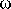 , où
, où 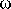 est la vitesse
angulaire actuelle de rotation de la Terre, et
est la vitesse
angulaire actuelle de rotation de la Terre, et 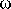 l'accélération
angulaire selon l'axe de rotation, est directement proportionnelle à
la dérivée temporelle du terme axial de degré 2 du développement en
harmoniques sphériques du champ de gravité. Ce terme est évalué
par les mesures de géodésie spatiale (tirs SLR sur les satellites de mesure du champ de gravité
Starlette et Lageos) à des valeurs comprises entre -2,5
+/-
0,3 10-11 /an
et -3,5 +/-0,3
10-11 /an (Peltier et Jiang, 1996; Rubincam, 1984).
l'accélération
angulaire selon l'axe de rotation, est directement proportionnelle à
la dérivée temporelle du terme axial de degré 2 du développement en
harmoniques sphériques du champ de gravité. Ce terme est évalué
par les mesures de géodésie spatiale (tirs SLR sur les satellites de mesure du champ de gravité
Starlette et Lageos) à des valeurs comprises entre -2,5
+/-
0,3 10-11 /an
et -3,5 +/-0,3
10-11 /an (Peltier et Jiang, 1996; Rubincam, 1984).
Les variations de la rotation de la Terre provoquées par la déglaciation affectent les
composantes du tenseur d'inertie (?) par le biais des effets de charge. La conservation
du moment d'inertie de la Terre nécessite un ajustement de la vitesse de rotation (de
composantes ?. Les deux quantités sont reliées entre elles par les
équations d'Euler, qui traduisent le principe de conservation. Dans un repère fixe
lié à la Terre, on peut écrire (Peltier et Jiang, 1996) :
où ? est le tenseur de Levi-Cevita. Si on suppose que ? reste
toujours très proche de sa valeur initiale ?, l'équation?
peut être linéarisée en introduisant le terme de perturbation :
où A, B, et C sont les trois moments d'inertie principaux, les
perturbations adimensionnées des composantes de la vitesse angulaire ?,
et les perturbations d'inertie.
En substituant ? dans ? on obtient :
avec les fonctions d'excitation données par :
La première étape dans le calcul de l'effet de charge sur ?
consiste à évaluer les expression de ?, ? et ?.
Pour un modèle visco-élastique, la perturbation d'inertie
est la somme d'un terme dit ;SPMlt;;SPMlt; de Terre rigide;SPMgt;;SPMgt; résultant
du seul effet de la charge de surface (indépendant de la rhéologie)
et un terme provenant de la déformation terrestre due à l'effet de
charge. La part rigide inclut la contribution de la glace et de l'océan.
Si on considère que la charge en surface est sur une couche très fine
par rapport au rayon de la Terre, on peut approcher le terme rigide
de la perturbation d'inertie par :
en intégrant sur toute la surface de la Terre, dont a est le rayon moyen
en harmoniques sphériques
on obtient pour le terme ? :
ce qui signifie que les coefficients de degré 2 de la charge de glace et de l'océan
suffisent au calcul.
Pour exprimer ? en fonction de ?, il suffit ensuite de résoudre
l'équation ? avec la perturbation ? donnée par :
dans laquelle ? est la convolution de ? par
le nombre de Love de degré 2. Ce nombre de Love de degré 2 est
donné par :
En substituant cette dernière expression dans l'équation ? et en intégrant,
on obtient l'expression de ? :
? se déduit de ? par le biais d'une constante multiplicative :
M est la masse de la Terre.
La figure de Peltier et Jiang, 1996, récapitule les valeurs du
? actuelles observées, à partir
des analyses des données anciennes d'éclipses pour Stephenson, 1995, à partir
d'observations satellitaires pour les autres.
L'expression explicite du mouvement du pôle
est plus difficile à obtenir. Il s'agit toujours de résoudre le système
des équations en tenant compte de ?. Le moyen de plus
simple semble être l'utilisation de la transformée de Laplace, et la
résolution dans le domaine de Laplace de ces équations sous la forme de ?,
ce qui donne, dans le domaine temporel :
où le symbole ? désigne le produit de convolution.
Les fonctions ?, ?, H' et H'' ont pour expression, dans le domaine
de Laplace :
avec
et
? est le nombre de Love fluide de degré 2 défini par ?,
et ? est le nombre de Love de l'effet de marée de degré 2.
Il s'agit ensuite d'obtenir des expressions explicites pour les fonctions ?, ?,
H' et H'' dans le domaine de Laplace, puis d'obtenir leur valeur dans
le domaine temporel par une transformée inverse.
Tous les calculs exposés ici sont extraits de la thèse de M.N. Bouin, effectuée au laboratoire de géologie de l'ENS, sous la direction conjointe de Ch. Vigny (ENS) et C. Boucher (IGN), et soutenue le 14 Octobre 1999, devant un Jury composé de MM F. Barlier (président), K. Lambeck (rapporteur), M. Kasser (rapporteur), F. Remy (examinateur), B. Ambrosius (examinateur), C. Boucher, et Ch. Vigny.
|
 ,
,
 ,t).
Ce potentiel de marée terrestre au point de la surface terrestre
de latitude
,t).
Ce potentiel de marée terrestre au point de la surface terrestre
de latitude  , de longitude
, de longitude
 et à l'instant t,
la réponse de la Terre à ce potentiel s'écrira :
et à l'instant t,
la réponse de la Terre à ce potentiel s'écrira : ,
,  )
correspond aux harmoniques sphériques normalisées sur la surface de la Terre, et
où le symbole
)
correspond aux harmoniques sphériques normalisées sur la surface de la Terre, et
où le symbole  désigne l'opérateur
gradient à deux dimensions, soit :
désigne l'opérateur
gradient à deux dimensions, soit : =
=
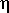 ,
LL
,
LL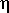 et
KL
et
KL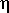 ,
où
,
où 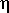 fait référence à
la rhéologie élastique adoptée, et L
au degré de la décomposition en harmoniques
sphériques, et désignent, respectivement, les coefficients d'harmoniques
sphériques des déplacements radial et tangentiel, et de la perturbation
gravitationnelle provoqués par la charge.
fait référence à
la rhéologie élastique adoptée, et L
au degré de la décomposition en harmoniques
sphériques, et désignent, respectivement, les coefficients d'harmoniques
sphériques des déplacements radial et tangentiel, et de la perturbation
gravitationnelle provoqués par la charge.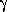 est un vecteur unitaire tangent à
la surface, selon le grand
cercle qui passe par le point de charge
(
est un vecteur unitaire tangent à
la surface, selon le grand
cercle qui passe par le point de charge
( ',
',
 ')
vers le point d'observation
(
')
vers le point d'observation
( ,
,  ), et
), et
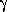 désigne la distance angulaire entre
les deux points.
désigne la distance angulaire entre
les deux points.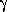 peut être donnée par :
peut être donnée par :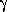 = cos
= cos cos
cos ' + sin
' + sin sin
sin ' cos(
' cos( -
- ')
')
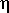 (
(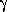 )
une fonction de Green, la réponse de la Terre à une masse surfacique
appliquée au point (
)
une fonction de Green, la réponse de la Terre à une masse surfacique
appliquée au point ( ',
',
 ') et au temps t
sera donnée par :
') et au temps t
sera donnée par :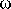 désigne la surface élémentaire autour du point (
désigne la surface élémentaire autour du point (
 ',
',
 ').
').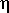 (
( ,
, ,t)
sera donc une quantité scalaire pour les
fonctions de Green radiale et de potentiel, et
un vecteur pour la réponse tangentielle correspondant à la fonction.
,t)
sera donc une quantité scalaire pour les
fonctions de Green radiale et de potentiel, et
un vecteur pour la réponse tangentielle correspondant à la fonction.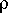 w est la densité de l'eau de
mer.
w est la densité de l'eau de
mer.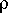 i est la densité de la
glace et où .
est la composante de degré L, et d'ordre
m de l'épaisseur
de la glace.
Pour la redistribution océanique, une première approximation est donnée
par la redistribution eustatique :
i est la densité de la
glace et où .
est la composante de degré L, et d'ordre
m de l'épaisseur
de la glace.
Pour la redistribution océanique, une première approximation est donnée
par la redistribution eustatique :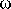 , où
, où 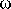 est la vitesse
angulaire actuelle de rotation de la Terre, et
est la vitesse
angulaire actuelle de rotation de la Terre, et 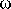 l'accélération
angulaire selon l'axe de rotation, est directement proportionnelle à
la dérivée temporelle du terme axial de degré 2 du développement en
harmoniques sphériques du champ de gravité. Ce terme est évalué
par les mesures de géodésie spatiale (tirs SLR sur les satellites de mesure du champ de gravité
Starlette et Lageos) à des valeurs comprises entre -2,5
+/-
0,3 10-11 /an
et -3,5 +/-0,3
10-11 /an (Peltier et Jiang, 1996; Rubincam, 1984).
l'accélération
angulaire selon l'axe de rotation, est directement proportionnelle à
la dérivée temporelle du terme axial de degré 2 du développement en
harmoniques sphériques du champ de gravité. Ce terme est évalué
par les mesures de géodésie spatiale (tirs SLR sur les satellites de mesure du champ de gravité
Starlette et Lageos) à des valeurs comprises entre -2,5
+/-
0,3 10-11 /an
et -3,5 +/-0,3
10-11 /an (Peltier et Jiang, 1996; Rubincam, 1984).