CHAMP DE TEMPERATURE
Considérons un volume de matière qui se trouve à une température T. une surface de ce volume est subitement porté à une température T + DT. Que va-t'il se passer ?
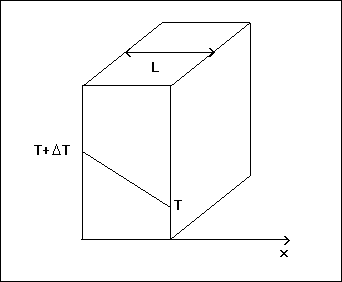
La chaleur va se propager de la face la plus chaude vers la face la plus froide pour équilibrer les températures par conduction. Cette propagation correspond à un flux q proportionnel au gradient de température.
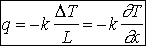
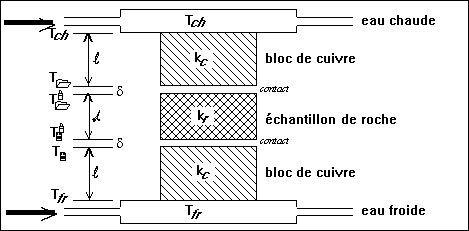
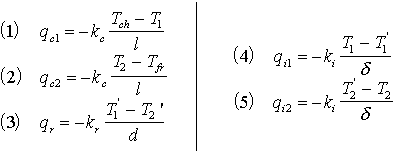
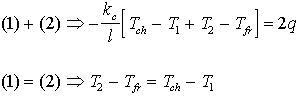
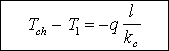
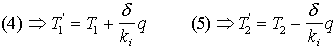
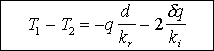
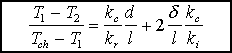
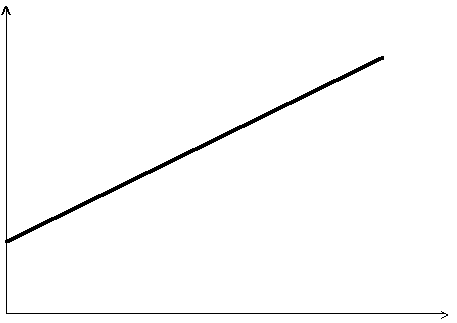
On peut donc dessiner la courbe des rapports de températures en fonction de d, l'épaisseur de l'échantillon de roche. c'est une droite de proportionnalité dont la pente est proportionnelle au rapport des conductivités et l'abscisse à l'origine dépend de la conductivité de l'interface machine/échantillon.
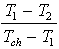 |  |
 |
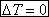
Considérons un volume de matière qui "baigne" dans un champ de température et qui est donc "traversé" par un flux de chaleur.
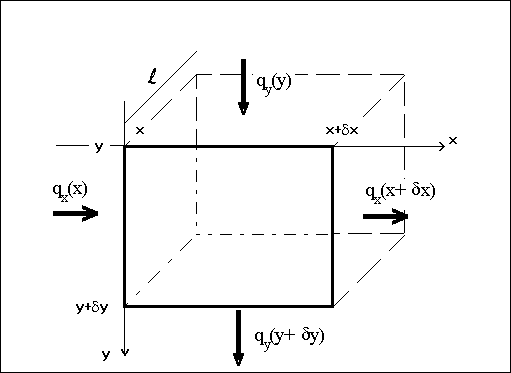
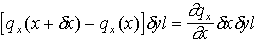
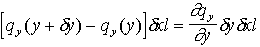
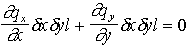
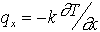 et
et 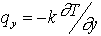 , on obtient finalement :
, on obtient finalement :
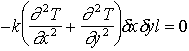
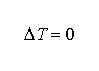
Un élément de matière a besoin d'un certain flux d'énergie par unité de temps pour maintenir un gradient de température. Or, La capacité calorifique (c) d'un milieu est la quantité d'énergie requise pour élever la température d'un gramme de matière de un degré. L'unité de c est donc : [c] = [E] / °K /kg.
Donc, si on considère un morceau de matière d'épaisseur dy et de densité 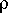 :
:
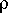 dy
dy
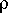 c dy
c dy
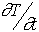
le flux d'énergie par unitéde temps nécessaire pour maintenir le taux de variation de la température est donc : 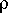 c dy
c dy 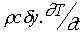 ( puisque E =
( puisque E = 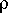 c dy dT)
c dy dT)
Si un flux d'énergie sors du morceau de matière, alors celui ci se refroidit, ce qui implique que le bilan net du flux de température qui le traverse 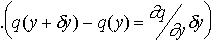 , n'est pas nul.
, n'est pas nul.
| On a donc : | 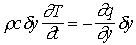 | => | 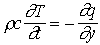 |
| => | 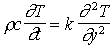 |
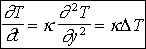 avec
avec 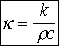
 est le coefficient diffusivité thermique.
est le coefficient diffusivité thermique. est : [
est : [ ] = [k] / [
] = [k] / [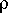 ][c]
][c]
| [k] = W m-1°K-1 = [E] s-1m-1°K-1 | |
[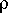 ] = kg m-3 ] = kg m-3 | => [ ] = m2 s-1 ] = m2 s-1 |
| [c] = [E] kg-1 °K-1 |
 pour se propager à la distance l. ou encore, se propagera à la distance
pour se propager à la distance l. ou encore, se propagera à la distance 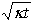 en un temps t.
en un temps t.
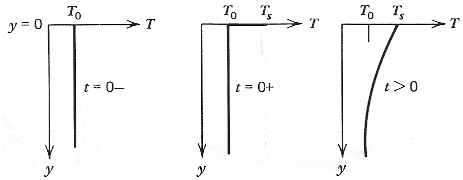
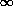
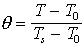 . l'équation de diffusion s'applique à
. l'équation de diffusion s'applique à  comme à T, mais les conditions aux limites sont plus simple.
comme à T, mais les conditions aux limites sont plus simple.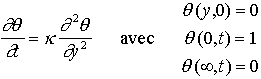
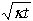 . Il est donc raisonnable de supposer que
. Il est donc raisonnable de supposer que  n'est pas une fonction de y et t séparement mais plutot une fonction du nombre sans dimension:
n'est pas une fonction de y et t séparement mais plutot une fonction du nombre sans dimension:
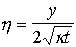
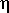 , il faut exprimer les dérivées partielles de
, il faut exprimer les dérivées partielles de  par rapport à t et y en fonction de
par rapport à t et y en fonction de 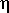 .
.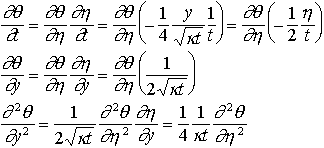
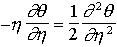
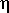 = 0 et y =
= 0 et y = 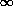 et t=0 devient
et t=0 devient 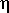 =
= 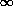 . On a donc :
. On a donc :  (
(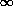 ) = 0 et
) = 0 et  (0) = 1.
(0) = 1.
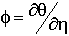 on obtient enfin pour l'équation de diffusion :
on obtient enfin pour l'équation de diffusion : 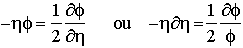
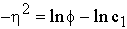
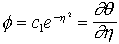
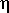 , on trouve :
, on trouve : 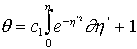
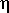 ' est une variable "muette" d'intégration, et la condition
' est une variable "muette" d'intégration, et la condition  (0)=1 a été utilisée pour trouver la deuxième constante d'intégration.
(0)=1 a été utilisée pour trouver la deuxième constante d'intégration.
 (
(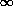 )=0), implique :
)=0), implique : 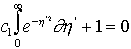
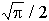 . On en déduit la constante :
. On en déduit la constante : 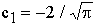
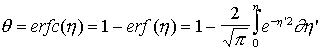
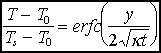
Les plaques tectoniques sont créées à partir de la matière mantellique chaude qui apparait en surface aux dorsales. Cette matière est refroidie et forme les plaques rigides (froides) de la tectonique des plaques. On identifie donc la "plaque" à la lithosphère océanique qui se déplace de manière rigide à la surface du manteau, et donc à la partie supérieure du manteau dont la température est trop faible pour que les roches se déforment sur les temps géologiques (les expériences de labo suggèrent environ 1500°K).
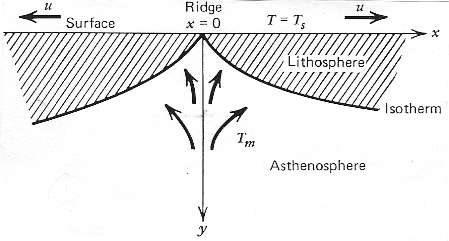
La base de la lithosphère est donc définie par un
isotherme donné. Sa profondeur augmente avec le temps (par diffusion, le
refroidissement se propage vers le bas). Donc la plaque s'épaissit en meme
temps qu'elle s'éloigne de la dorsale. donc au fur et à mesure de son
veillissement : t = x/u.
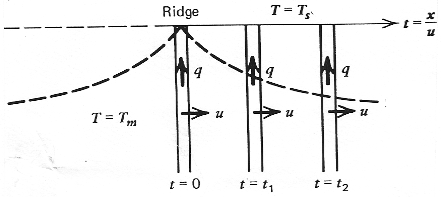
La température dans le manteau est Tm. La température
de refroidissement à la surface est imposée par l'eau et vaut Ts. Donc
une colonne de matière à x=0 qui a pour température Tm partout se voit
brutalement appliquer la température Ts à son sommet. Puis au fur et à mesure
qu'elle séloigne de la dorsale, la température de surface est maintenue à Ts,
et le refroidissement se propage vers le bas comme dans le problème du
refroidissement d'un demi espace infini.
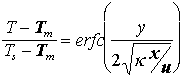
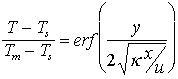
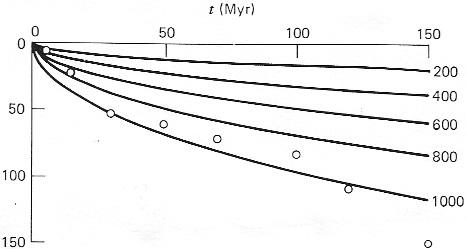
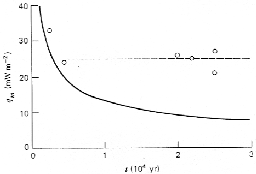
Différents isothermes (T-Ts), pour Tm-Ts = 1300°K (n'oublions pas que Ts ~ 300°K) et  = 1 mm2 s-1. Les points montrent l'épaisseur de la lithosphère différents endroit, determinée par sismologie.
= 1 mm2 s-1. Les points montrent l'épaisseur de la lithosphère différents endroit, determinée par sismologie.
| Si on cherche l'isotherme T=1500°K : | => | T-Ts ~ 1200°K |
| => | (T-Ts)/(Tm-Ts) ~ 0,9 | |
| => | 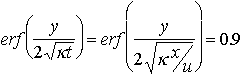 | |
| => | 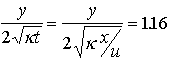 | |
| => | 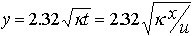 |
Pour les valeurs précédentes ( = 1 mm2 s-1) on trouve une épaisseur y =116 km à un age t = 80 MA, ou à une distance de la dorsale (u=10cm/an) x = 8000 km.
= 1 mm2 s-1) on trouve une épaisseur y =116 km à un age t = 80 MA, ou à une distance de la dorsale (u=10cm/an) x = 8000 km.
qs, le flux de chaleur en surface est donné par : 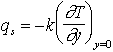
On a donc :
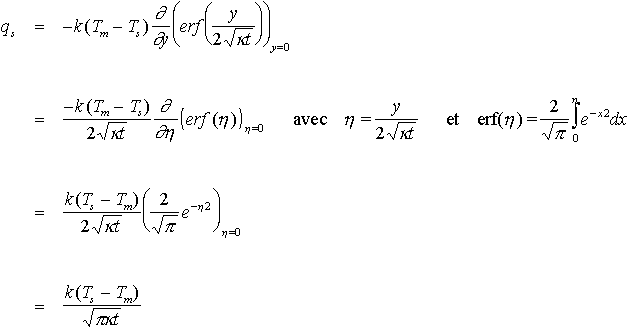
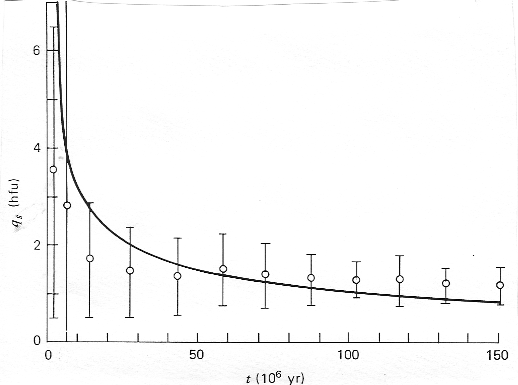
qs Avec les valeurs précédentes et k = 3.3 W/m/°K. Les points montrent les mesures de flux de chaleur en différents endroit des fonds océaniques (donnés en fonction de leur age).
e) Flux de chaleur terrestre
On peut mesurer l'age des fonds océaniques et en
déduire la courbe de la surface cumulative en fonction de cet age. Pour chaque
age, on regarde quelle est la surface de planchers océaniques (A) d'age
inférieur.
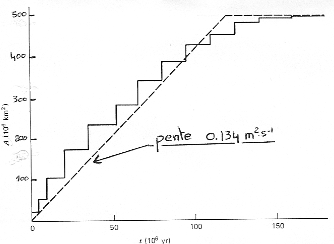
La courbe en escalier montre les surfaces mesurées
pour des ages de 5, 10, 20, 30, 40, 50, etc... million d'années. La courbe en
pointillé correspond à un modèle continu : dA/dt = 0.134 m2/s (puis
tout est subducté à 120.8 MA). L'age moyen est de 60.4 MA.
Le flux moyen du modèle à taux constant qui "colle" bien est :
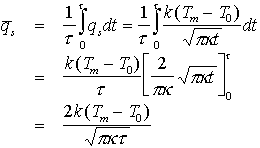
Avec les valeurs précédentes ( ,
,  , k, T), on trouve : qs = 78.5 mW.m-2. Ce qui correspond assez bien à la valeur moyenne mesurée (78.2). On en déduit donc qu'une fraction substentielle de l'évacuation de la chaleur terrestre s'effectue par refroidissement de la lithosphere océanique.
, k, T), on trouve : qs = 78.5 mW.m-2. Ce qui correspond assez bien à la valeur moyenne mesurée (78.2). On en déduit donc qu'une fraction substentielle de l'évacuation de la chaleur terrestre s'effectue par refroidissement de la lithosphere océanique.
Le geotherme qui correspond à un age de 60.4 MA (age moyen de la lithosphere océanique) est le suivant :
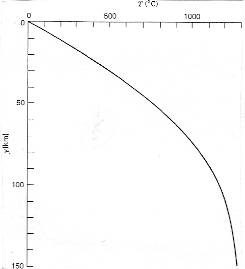
Si on applique les équations à la lithosphère
continentale il faut tenir compte de la production de chaleur dans la croute.
Pour simplifier, on utilise le flux de chaleur réduit, c'est à
dire uniquement la contribution mantellique au flux
de chaleur en surface. Pour déterminer sa valeur à la surface de la Terre, il
faut utiliser la corrélation entre la concentration d'isotopes radioactifs et
le flux de chaleur mesuré en surface...