HARMONIQUES SPHERIQUES
1/ Opérateurs classiques en coordonnées sphériques 2/ Harmoniques sphériques a/ Résolution de l'équation de Laplace b/ Décomposition d'un champ sur la base des harmoniques sphériques c/ Spectre d'un champ d/ Corrélation entre deux champs e/ Application à la topographie terrestre
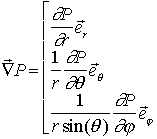
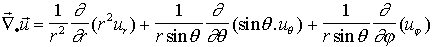
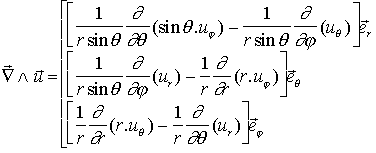
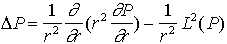
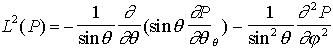
Un champ quelconque sur une sphère doit satisfaire l'équation de Laplace loin des sources (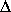
P = 0). donc si on cherche une base sur laquelle exprimer ce champ P, les "fonctions-vecteurs" de cette base doivent aussi satisfaire cette équation. On doit donc chercher les fonctions V(r,
,
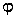) qui satisfont 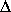V = 0.
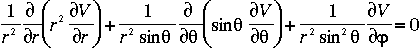
On suppose que la solution présente des variables séparées : V(r,,) = R(r) . 
() . 
()
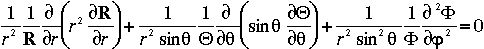
la première partie est indépendante de et 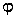, la seconde partie est indépendante de r. Chaque terme doit donc être égal à une constante sans dimension dont la somme pourra s'annuler.
pour le 1er membre :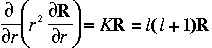 
en cherchant des fonctions polynomes du type : R=ra, on trouve pour solution :
R = K(rl + r-(l+1) )
pour le 3me membre :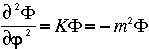 
en cherchant des fonctions trigonométriques du type :
= e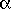 
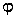, on trouve pour la
solution :
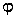() = K e im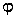
En remplaçant R et , l'équation du Laplacien devient une équation en seulement, que l'on peut écrire :
|
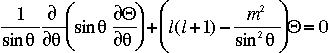
Avec x = cos()
|
=> |
d/d = d/dx . dx/d = d/dx . sin
|
| => |
sin2 = 1 - cos2 = 1-x2
|
On obtient :
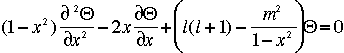
Les fonctions solutions de cette équation sont les polynomes de Legendre, qui n'existent que pour des valeurs entières et positive de l et des valeurs entières de m entre -l et +l. Ces polynomes s'écrivent :
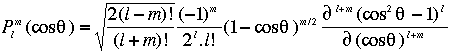
En fait ces fonctions sont moins compliquées qu'il n'y parait puisque ce sont tout simplement des produits de sinus et cosinus de puissances l et m. La table suivante donne les premiers polynomes de Legendre.
| P00(cos) | = | 1 |  |
| P10(cos) | = | cos |  |
| P11(cos) | = | -sin | |
| P20(cos) | = | 1/2(3cos2 - 1) |  |
| P21(cos) | = | -3cos | |
| P22(cos) | = | 3sin2 | |
| P30(cos) | = | 1/2cos(5cos2 - 3) |  |
| P31(cos) | = | 3/2sin(-5cos2 + 1) | |
| P32(cos) | = | 15cossin2 | |
| P33(cos) | = | -15sin3 | |
Il est assez facile de se rendre compte que chaque Polynome de Legendre passe un certain nombre de fois par zero quand | |||
Les fonctions solutions de l'équation de Laplace sont donc finalement les harmoniques sphériques Ylm, qui s'écrivent donc :
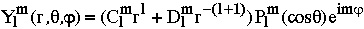
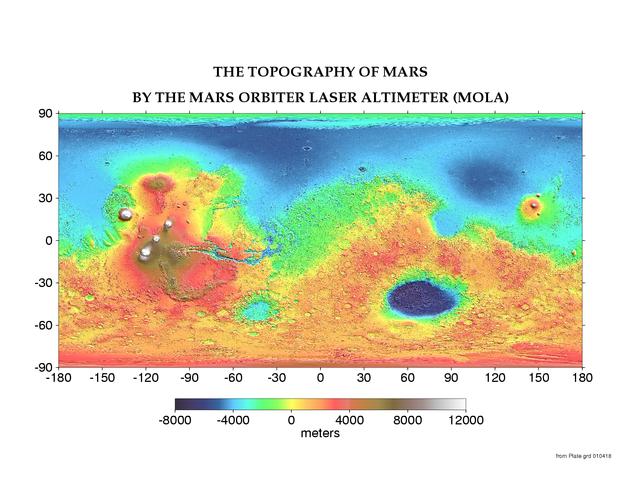
Pour un champ que l'on peut definir sur une surface sphérique (r=constante), par exemple la topographie terrestre, on supprime la dépendance en r pour obtenir les harmoniques sphériques surfaciques :
|
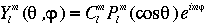
La figure ci-dessus montre les fonctions harmoniques sphériques de degré et d'ordre variables. Ce sont donc des surfaces qui enveloppent la sphère et qui présentent des ondulations de part et d'autre de zero. en rouge les zones positves, en bleu les zones négatives, et en blanc les passages par zero. la règle est que la fonction harmonique sphérique passe autant de fois par zero que ce que vaut son degré l. Parmi ces passages par zero, m se font suivant un longitude (sur un grand cercle), et donc l-m suivant une latitude (sur un petit cercle).
C'est logique : l est l'exposant total des produits de sinus et cosinus qui forment le polynome de Legendre. Par exemple, le polynome Pl=3m=1 qui contient cos2.sin est une fonction de degré 3 (l=3), et s'annule 2 fois (l-m=2) pour variant entre 0 et 
(c'est le cosinus qui a deux racines). pour obtenir l'harmonique il faut multiplier par eim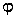 qui elle s'annule une seule fois (m=1) sur la sphère.
En résumé en assimilant un passage par zero à un "coup de couteau" au travers de la sphère (les zones blanches sur les figures donc) :
- il y a l coups de couteau dans la sphère
- parmi eux m sont "verticaux" (suivant une longitude)
- et l-m sont "horizontaux" (suivant une latitude)
Tout champ qui a un Laplacien nul peut donc "s'écrire" sur la base des harmoniques sphériques :
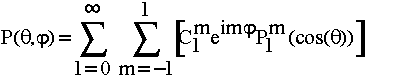
En fait, Clm est un nombre complexe tel que : Clm = (alm +i blm) et l'exponentielle complexe eim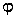 s'exprime aussi : eim 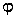= cos(m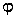) + i sin(m).
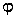On obtient donc :
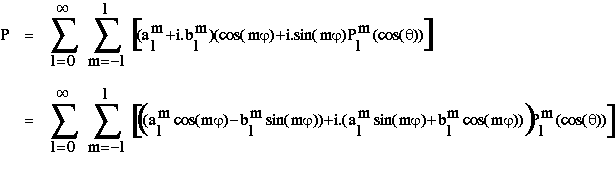
P étant un champ réel, il est clair que le terme imaginaire de la recomposition doit toujours être nul. Cela impose que la somme sur l et m des termes imaginaires soit nulle. La somme pour m allant de -l à l peut être réécrite comme une somme pour m de -l à 1, 0, et 1 à l. On obtient alors :
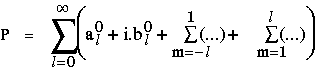
Il est facile de voire que pour les valeurs positive et négatives de m, les termes imaginaires en i(almsin(m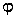) + blm cos(m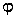)) vont s'annuler 2 à 2 à condition que : al-m = alm et bl-m = -blm ; et que pour les terme m = 0 (al0+ i.bl0) il faut tout simplement
que bl0 = 0. La décomposition du champ P se réduit donc à une nouvelle somme :
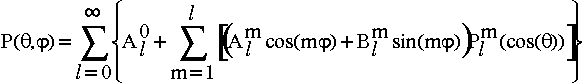
Alm et Blm sont les coefficients de ce champ, tout comme une courbe à une dimension peut être représentées par la suite infinie de ses coefficients dans une décomposition en série de Fourier de Fourier. l est le degré, m est l'ordre.
Dans une décomposition en série de Fourier, la longueur d'onde associée à un coefficient de degré n est : 
= L/n (le degré 1 donne toute la longueur L, le degré 2 la moitié, etc...). De manière similaire, dans une décomposition en harmoniques sphériques, on associe une longueur d'onde 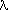au degre l. A la surface de la Terre, on a :
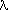= 2RT / l le degré 1 correspont à une longueur d'onde de 36000 km (la circonférence de la Terre, le degré 2 à 18000 km, le degré 10 à 3600 km, etc...
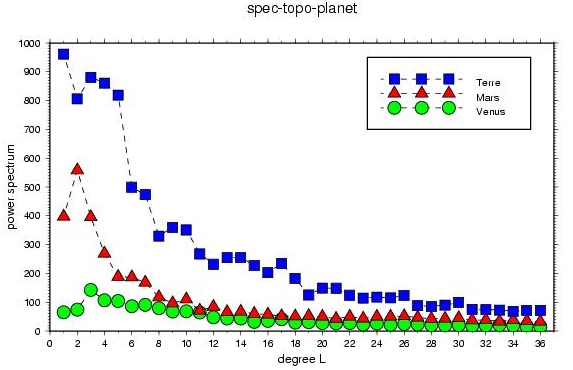
Le spectre d'un champ est la suite infinie de nombre qui donne l'amplitude de chacun des termes de degré l de la décomposition du champ.
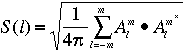
Un coefficient S(l) élevé indique que la contribution de ce degré dans le champ total est élevé. Pour un champ dont tous les coefficient S(l) sont du meme ordre de grandeur, on parle de spectre plat.
La figure ci-dessus montre le spectre d'un champ quelconque (en fait ici la topographie terrestre). On porte tout simplement la valeur de coefficient S(l) en fonction de l... Les unités sont donc les degrés harmoniques sphériques en abscisse, et des mètres en ordonnée. On voit que la courbe est décroissante, ce qui veut dire que les bas degrés (les longueurs d'onde élevées) sont de plus forte amplitude que les degrés élevés (les courtes longueur d'onde)
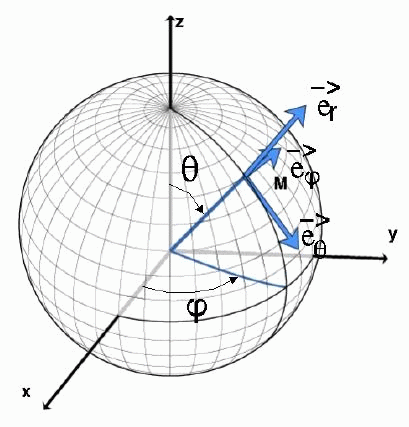
On a deux champs (A et B) définis en tous points sur la sphère ( et 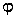). La décomposition sur la base des harmoniques sphériques de ces deux champs est constituées des deux suites de nombres complexes Alm et Blm. le coefficient de corrélation entre les deux champs au degré l est :
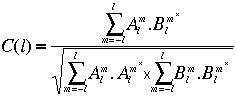
Si C(l)=1 alors les coefficients des champs A et B au degré l sont proportionnels. Pour que les deux champs A et B soient complètement identiques, il faut que tous les coefficients de corrélation valent 1 et que les coefficients de proportionnalité de tous les degrés valent 1 aussi.
C(l)=1 (ou = -1) implique qu'il y a 100% de chance que les deux champs soient parfaitement corrélés (ou anti-corrélés) au degré l considéré.
Plus précisement :
au degré l il y a N=2l+1 termes (m varie de -l à l). Le coefficient de corrélation est r = C(l). Or, dans un problème à N degrés de liberté, la probabilité pour que la variable t = 
(N/1-r2) soit plus petite qu'une certaine valeur donnée t0, est la student's t-distribution: Q(t,N). La valeur 1-Q(t,N) est donc le niveau de confiance auquel l'hypothèse d'une corrélation due au hasard est infirmée.
Par exemple : r=1 => t =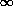 
(qqsoit N) => Q(t,N) = 0 => 1 - Q(t,N) = 1 = 100%
C(l)=1 => il y a 100% de chance que la corrélation entre les champs A et B au degré l ne soit pas due au hasard
La figure ci-dessus montre une courbe de corrélation fictive entre deux champs, avec les niveaux de confiance à 80%, 90%, et 95%. Un coef. de corrélation égal à l'une de ces valeurs indique qu'il y a 80%, 90%, ou 95% de chances pour que la corrélation à ce degré ne soit pas due au hasard. La figure ci-dessus montre une carte de la topographie terrestre "telle qu'elle est", c'est à dire, une valeur d'altitude toutes les 10 minutes (6 points par degré). On obtient une grille de 1080x2160 points, c'est à dire 2,332,800 points ! La figure ci-dessus montre une carte de la topographie terrestre après qu'elle ait été décomposée sur la base des harmoniques sphériques jusqu'au degré l = 36. on voit qu'on obtient quelque chose de raisonnablement ressemblant à partir de seulement 1406 coefficients (tous les coefficients harmoniques sphériques de l=0 à 36 (l+1)(l+2)) !
Jouons un peu avec les coeeficients harmoniques sphériques de la topographie Terrestre Reconstitutions de la topographie terrestre du degré 0 jusqu'à un degré à chaque fois plus élevé (6, 16, puis 36). Plus on va loin, plus la "qualité" de la représentation est bonne. filtrages de la topographie terrestre dans certaines "gammes" de degrés (donc de longueur d'onde. de 6 à 36 puis de 16 à 36. dans ces cas là, le champ est à la fois un peu lissé (pas de courtes longueurs d'onde correspondant à des degrés supérieurs à 36) et dégagé des effets à grande longueur d'onde. on voit donc les ondulations de taille caractéristique entre ces deux filtres passe haut et passe bas.
Comment analyser la courbe ci-dessus ?
La première chose que l'on peut noter est qu'il y a deux "domaines" :
- les bas degrés (l < 10) : tous les coefficients sont proche de zero, et en tous cas largement en dessous de la courbe à 80% de confiance. cela veut dire que pour ces grandes longueurs d'onde, il n'y a pas de corrélation significative entre ces deux champs.
-les degrés plus élevés (l > 10) : tous les coefficients sont au dessus de la courbe à 95% de confiance. Cela signifie qu'il n'y a qu'une toute petite chance (de l'ordre de quelques %) pour que la ressemblance entre les deux champs soit due au hasard, et que donc ils sont significativement corrélés à courte longueur d'onde (grand degré).
On pourrait en déduire que la source à l'orgine des deux champs est distincte à grande longueur d'onde (ce n'est pas le meme phénomène qui est à l'origine des deux champs), et peut etre commune à courte longueur d'onde...
e) Application à la topographie terrestre
Evidemment, la carte est un peu "lissée", c'est à dire que les détails les plus fins, de taille caractéristique inférieure à 1000 km (l=36 => =1000 km), sont éliminés par le fait que l'on arrete la décomposition en harmoniques sphériques à ce niveau là. C'est un peu comme si un géant palpait la Terre avec des doigts de 1000 km de largeur : il ne pourrait pas sentir les creux et les bosses plus petits que ses doigts ...
Les premiers coefficients de la décomposition de la topographie terrestre en harmoniques sphériques l m alm blm 0 0 -8152 0 1 0 2265 0 1 1 -1481 1025 2 0 1825 0 2 1 -842 764 2 2 -1039 201 3 0 -616 0 3 1 336 287 3 2 -1115 -1145 3 3 -290 1363 4 0 1316 0 4 1 554 -623 4 2 -955 -140 4 3 -899 -293 4 4 -141 -1119 5 0 -1948 0 5 1 118 -135 5 2 -36 392 5 3 -355 65 5 4 1277 161 5 5 167 568 6 0 830 0 6 1 2 -425 6 2 20 284 6 3 -157 479 6 4 449 418 6 5 228 -514 6 6 102 -51 Décompositions de la topographie terrestre degré par degré, de 0 à 6
degré l = 0
degré l = 1
degré l = 2
degré l = 3
degré l = 4
degré l = 5
degré l = 6
reconstitution
de l = 0 à 6
reconstitution
de l = 0 à 16
reconstitution
de l = 0 à 36
filtrage pour
l entre 6 et 36
filtrage pour
l entre 16 et 36
Retour au sommaire du cours
