Avertissement : ceci est un petit traité mathématique sur la théorie du traitement des données GPS (d'après R.W. King et al., 1985). Il y est notament expliqué comment s'affranchir des erreurs ou imprécisions d'horloges pour obtenir un positionnement précis (différentiel). L'impact de l'Ionosphère est également expliqué, et l'utilité du GPS bi-fréquence pour s'en affranchir est exposée et détaillée. Des graphiques montrant des données typiques sont commentés.
La donnée que l'on récupère à la sortie d'un
récepteur GPS est la différence entre la phase de l'onde émise par un satellite et la phase d'un oscillateur interne au récepteur. La phase de l'onde reçue est affectée par l'effet Doppler du au déplacement du satellite, la réfraction atmosphérique, et le bruit de mesure du récepteur. On peut écrire la différence de phase  ij(tj), au temps t, à la station j, et pour le satellite i, comme suit :
ij(tj), au temps t, à la station j, et pour le satellite i, comme suit :
 ij(tj) =
ij(tj) =  ijr -
ijr -  jl + nij +
jl + nij +  bruit
bruit ijr : phase reçue à la station j en provenance du satellite i
ijr : phase reçue à la station j en provenance du satellite i jl : phase de l'oscillateur du récepteur j
jl : phase de l'oscillateur du récepteur j bruit : bruit aléatoire sur la mesure de phase
bruit : bruit aléatoire sur la mesure de phasePar ailleurs, le signal reçu au temps tj est lié au signal émis au temps ti par le ième satellite par la relation suivante:
 ij(tj)
ij(tj) dans laquelle  ij est le temps de propagation qui dépend de la géometrie satellite-station, et des perturbations ionospheriques et tropospheriques.
ij est le temps de propagation qui dépend de la géometrie satellite-station, et des perturbations ionospheriques et tropospheriques.
On en déduit que la phase du signal reçu au sol est relié à la phase transmise par le satellite par:
 ijr(tj) =
ijr(tj) =  it(tj -
it(tj -  ij)
ij) Il nous faut maintenant "modéliser" la phase  de l'oscillateur du satellite. C'est à dire "savoir" ce qu'elle vaut en fonction de la fréquence de cet oscillateur.
de l'oscillateur du satellite. C'est à dire "savoir" ce qu'elle vaut en fonction de la fréquence de cet oscillateur.
Modélisation de l'oscillateur du satellite : ( it)
it)
Bien sur, un oscillateur n'est jamais stable dans le temps !
On devrait avoir :
 it(t+
it(t+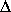 t) =
t) =  it(t) +
it(t) + 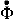 it(t)
it(t)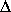 t
t Par cette équation, on écrit simplement que l'évolution de la phase avec le temps est linéaire. La phase  augmente avec le temps : à un instant t+
augmente avec le temps : à un instant t+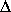 t elle vaut ce qu'elle valait à l'instant t, plus la quantité dont elle a augmenté pendant le temps
t elle vaut ce qu'elle valait à l'instant t, plus la quantité dont elle a augmenté pendant le temps 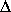 t.
t.
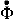 est le taux d'accroissement de la phase (ou encore la dérivé de la phase) par rapport au temps.
est le taux d'accroissement de la phase (ou encore la dérivé de la phase) par rapport au temps.
Et en fait, on a une expression plus complexe avec des termes supplémentaires :
 it(t+
it(t+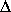 t) =
t) =  it(t) +
it(t) + 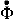 it(t)
it(t)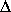 t +
t + 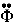 it(t)
it(t)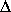 t2 + ...
t2 + ... dans laquelle 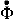 et
et 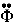 représentent respectivement le taux de changement de la phase (la fréquence), et l'accélération de ce taux (la dérive de la fréquence). On néglige les termes suivants (l'accélération de la dérive par exemple).
représentent respectivement le taux de changement de la phase (la fréquence), et l'accélération de ce taux (la dérive de la fréquence). On néglige les termes suivants (l'accélération de la dérive par exemple).
On a donc, pour la phase "One-way" :
 ij(tj) =
ij(tj) =  it(tj) -
it(tj) - 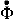 it(tj)
it(tj) ij(tj) +
ij(tj) + 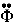 it(tj)
it(tj) ij2(tj) -
ij2(tj) -  jl(tj) + nij +
jl(tj) + nij +  bruit
bruit où t0 est une "époque" de référence située quelque part pendant la transmission. La fréquence nominale f0 est la même pour tous les satellites, le décalage initial ai "offset" et la dérive bi "drift" sont propres à chaque oscillateur.
Il faut intégrer la fréquence pour obtenir la phase, on a donc :
tj | |||||
| = |
| + | [ f0 + ai + bi(t-t0) ] dt | |
t0 | |||||
= |
| + | (f0 + ai)(tj-t0) + |
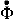 it(tj) = [d
it(tj) = [d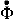 / dt ]tj = fi(tj) = f0 + ai + bi(tj-t0)
/ dt ]tj = fi(tj) = f0 + ai + bi(tj-t0)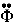 it(tj) = [d2
it(tj) = [d2 / dt2 ]tj = [ dfi / dt ]tj = bi
/ dt2 ]tj = [ dfi / dt ]tj = bi il)
il)
tj | ||||||||
| = |
| ||||||
t0 | ||||||||
= |
| |||||||
| = | - (f0 + ai + bi(tj-t0)) |
+ | ||
- | ||
+ nij + |
Seuls les termes de la 1ière ligne dépendent du temps de parcours  ij et donc de la distance satellite-station.
ij et donc de la distance satellite-station.
Le premier terme est simplement le produit de la fréquence modélisée de l'émetteur par le temps de propagation. le deuxième terme quadratique est faible et peut être négligé.
Les effets de l'instabilité des horloges des satellites et des récepteurs apparaissent dans les lignes 2, 3, et 4.
La combinaison des premiers termes des lignes 2 et 3 représente la différence de phase entre les deux oscillateurs aux temps t0. Cette différence de phase est différente de "l'ambiguïté entière" nij qui représente le nombre inconnu d'oscillations entières entre le satellite et la station.
Les seconds termes des lignes 2 et 3 peuvent disparaitre si la fréquence nominale de l'oscillateur de la station est exactement égale à la fréquence nominale f0.
Les termes restants représentent les erreurs de mesure dues aux fluctuations des horloges des satellites et des récepteurs, plus un certain bruit inhérent aux mesures de phase ( bruit)
bruit)
En combinant les données obtenues à deux stations différentes pour le même satellite j, on peut éliminer le principal des erreurs provenant de la dérive de l'horloge du satellite considéré. En effet, en prenant f0 = fj1 = fj2, on obtient :
| = |
| = | - f0( |
- (ai + bi(t-t0))( | ||||
- f0(r2-r1)(t-t0) - | ||||
- [ | ||||
+ |
La première ligne représente l'effet géométrique.
La deuxième ligne contient la dérive de l'horloge du satellite qui est faible (les termes quadratiques en (t-t0)2 ont été éliminés par la différenciation.
La troisième ligne contient les effets des horloges des deux récepteurs qui sont les erreurs les plus importantes.
La quatrième ligne contient les différences de phase initiale entre les deux oscillateurs des récepteurs au temps t0 (incluant un terme représentant l'offset des horloges), ainsi que la différence des ambiguïtés.
On peut faire les mêmes différences entre satellites pour une station donnée, qui vont donner une observable affranchies des erreurs provenant des horloges des stations. Mieux encore, on peut différentier entre satellites l'observable différentiée entre stations, et s'affranchir des erreurs provenant des horloges des satellites et des stations. C'est le principe de la double-différence. On obtient alors :
| = |
| = | - f0( |
- (a2 + b2(t-t0))( | ||||
+ (a1+b1)(t-t0))( | ||||
+ (n22 - n21 - n12 - n11) + |
l'effet géométrique représenté par le produit de
la fréquence nominale et des temps de propagation apparait en
ligne 1. Les lignes 2 et 3 contiennent des quantités dépendant
de la dérive des horloges des satellites (faible à
priori) multipliées par les différences des
temps de parcours (quantité faible devant le temps de parcours
lui même). Ces quantités seront d'autant plus faibles
que les distances entre stations seront faibles. La quatrième
ligne contient les ambiguïtés entières (le nombre
entier inconnu d'oscillations entre satellite et récepteur. les
différences de phases initiales entre satellites et recepteurs
ont été éliminées.
L'Ionosphère est un "nuage" de particules chargées (ions et électrons) qui enveloppe la Terre entre 70 et 2000 km d'altitude. Les ondes émises par les satellites GPS orbitant à 20000 km d'altitude doivent donc traverser cette couche avant d'arrivée sur la Terre. Le signal GPS est perturbé comme toute onde électromagnétique traversant un milieu conducteur. Cette perturbation se manifeste par un retard, c'est à dire que la vitesses de propagation de l'onde dans ce milieu conducteur qu'est l'Ionosphère est plus faible que ce qu'elle serait dans le vide. Le temps de propagation de l'onde est donc plus long que ce qu'il serait dans le vide, ce qui conduit à surestimer la longueur de la distance satellite-station.
si l'onde GPS se propageait dans le vide, la phase vaudrait :
 = (f.r) / c
= (f.r) / c
Du fait de la propagation dans un milieu conducteur (l'Ionosphère) il faut considerer une perturbation. Au premier ordre, l'Ionosphère peut etre considérée comme un milieu dispersif, c'est à dire que le retard induit est inversement proportionnel au carré de la fréquence de l'onde. Sur la phase, cela se traduit par un décalage qui est inversement proportionnel à la fréquence de l'onde. On peut donc écrire la phase :
 = (f.r) / c -
= (f.r) / c - 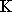 / f
/ f 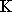 est un nombre qui dépend de la conductivité de l'ionosphère, c'est à dire de la densité d'électrons et d'ions dans ce milieu.
est un nombre qui dépend de la conductivité de l'ionosphère, c'est à dire de la densité d'électrons et d'ions dans ce milieu.
Le problème vient du fait que ce nombre 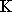 est en général inconnu et très variable dans le temps. En effet, l'ionosphère est sujette à des courants électro-magnétiques violents, à des tempetes de particules chargées, tout cela en relation avec les flux de particules qui nous viennent du soleil: les "vents" solaires. Il est donc à priori impossible de connaitre le décalage de phase induit par l'ionosphère sur une fréquence donnée. Heureusement, le décalage dépendant de la fréquence, il est possible de contourner le problème en émettant sur deuxfréquences différentes. La comparaison de l'effet sur chacune des fréquences permet alors de le quantifier, et donc de l'éliminer.
est en général inconnu et très variable dans le temps. En effet, l'ionosphère est sujette à des courants électro-magnétiques violents, à des tempetes de particules chargées, tout cela en relation avec les flux de particules qui nous viennent du soleil: les "vents" solaires. Il est donc à priori impossible de connaitre le décalage de phase induit par l'ionosphère sur une fréquence donnée. Heureusement, le décalage dépendant de la fréquence, il est possible de contourner le problème en émettant sur deuxfréquences différentes. La comparaison de l'effet sur chacune des fréquences permet alors de le quantifier, et donc de l'éliminer.
On écrit donc
 1 = (f1.r) / c -
1 = (f1.r) / c - 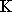 / f1
/ f1  2 = (f2.r) / c -
2 = (f2.r) / c - 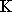 / f2
/ f2 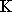 ), en faisant une combinaison linéaire (
), en faisant une combinaison linéaire ( C) de
C) de  1 et
1 et  2 :
2 : C = f12 /(f12-f22) (
C = f12 /(f12-f22) (  1 - f2 / f1
1 - f2 / f1  2 )
2 )
 1 et
1 et  2 par leur expression en fonction de f1 et f2, on obtient aisément :
2 par leur expression en fonction de f1 et f2, on obtient aisément : C = f12 / (f12-f22) . (f12-f22) / f1 . (r/c) = f1 . r/c
C = f12 / (f12-f22) . (f12-f22) / f1 . (r/c) = f1 . r/c
 1 et
1 et  2), on élimine l'effet de l'Ionosphère (au premier ordre au moins), et qu'on a bien une "phase virtuelle"
2), on élimine l'effet de l'Ionosphère (au premier ordre au moins), et qu'on a bien une "phase virtuelle"  C qui se comporte comme si l'onde 1 se propageait dans le vide.
C qui se comporte comme si l'onde 1 se propageait dans le vide.
Le point physique où se matérialise l'onde GPS qui arrive sur l'antenne réceptrice est appelé le centre de phase de l'antenne. Le problème est que ce point est immatériel, que sa localisation au millimètre près est très difficile, et qu'en plus sa position a tendance à dépendre de l'angle incidence et de l'azimut du signal. Il apparait donc que l'on ne mesure pas la position d'un point fixe : le centre géométrique de l'antenne, mais la position d'un point mobile dans un espace qui peut aller jusquà 10mm de rayon. Il n'y a pas d'autre solution que de calibrer parfaitement chaque antenne, afin d'établir une cartographie précise de la position du centre de phase en fonction de l'azimut et de l'élévation du signal incident. Cette "fonction d'appareil" devra etre appliquée à chaque mesure de phase.
En pratique, de telles calibration sont extrèmement difficiles à réaliser. On procède donc de manière relativement empirique : en n'utilisant que des antennes identiques, toutes alignées dans la meme direction. si la position de chaque antenne varie dans le temps, la distance entre les antennes reste bien invariable, le centre de phase de toutes les antennes se déplaçant en meme temps de la meme quantité dans le meme direction.
Il ne faut pas oublier que le GPS est un système conçu par et pour les militaires américains. En conséquence, un certain nombre de moyens ont été mis en place pour empecher l'utilisation du système par un hostile. Ce but est atteint par la dégradation volontaire de la précision du positionnement pour tout utilisateur non autorisé.
La "Selective Availability" (SA)
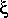 est donnée par :
est donnée par :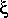 = xa + dx
= xa + dx | Sa position est donnée par le vecteur | : | xt0m |
| Sa "distance" dans le temps et dans l'espace par rapport à une origine arbitraire est donnée par | : | 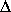 xt0m = xt0m - xt00 xt0m = xt0m - xt00 |
| A ti, on a | : | 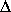 xtim = xtim = 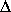 xt0m + (ti - t0) um xt0m + (ti - t0) um |
| . | . | ||||
| relation dans laquelle : | L | = | E | + | W |
| | | ||||
| partie symétrique taux de déformation | partie antisymétrique taux de rotation |
| . | . | E11 | E12 | . | |||
| E | = |  (L + LT) (L + LT) | = | ||||
| E21 | E22 |
| . | . | 0 | W | . | |||
| W | = |  (L - LT) (L - LT) | = | ||||
| -W | 0 |
 1,
1,  2, et
2, et  .
.  1 et
1 et  2 sont les taux d'extension et de compression suivant les directions principales définies par l'angle
2 sont les taux d'extension et de compression suivant les directions principales définies par l'angle  entre la direction
entre la direction  2 et le Nord.
2 et le Nord. 1 = E11 cos2
1 = E11 cos2 + E22 sin2
+ E22 sin2 - 2 E12 sin
- 2 E12 sin cos
cos
 2 = E11 sin2
2 = E11 sin2 + E22 cos2
+ E22 cos2 - 2 E12 sin
- 2 E12 sin cos
cos
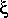 m.
m.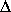 xm, on a :
xm, on a : 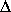
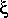 m =
m = 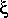 m -
m - 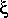 0
0
| Les vitesses | . | E | s'écrivent | . | Cme | avec : | ||
W | Dmw |
e = | . | E11 | . | et w = W12 | ||
E22 | ||||||
E12 | ||||||
| INCONNUES | ||||||
L'ajustement sur la position de la station m au temps ti est donc :
| = |
| ||
| ajustement des positions initiales de l'origine et de la station m | déplacement de la station m au cours du temps |
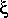 . C'est en minimisant cet ajustement que l'on obtiendra les taux de déformation et de rotation qui "expliquent au mieux" les données. Pour cela, on dispose d'un jeux de M équations (autant que de stations) à un temps donné. Puis autant de jeux que d'époques de mesures.
. C'est en minimisant cet ajustement que l'on obtiendra les taux de déformation et de rotation qui "expliquent au mieux" les données. Pour cela, on dispose d'un jeux de M équations (autant que de stations) à un temps donné. Puis autant de jeux que d'époques de mesures.